题目内容
15．菱形有一个内角是120°，较短的一条对角线长为6，则此菱形的边长是6，菱形的面积是18$\sqrt{3}$．分析 作出草图，根据菱形的邻角互补求出菱形的锐角为60°，然后求出△ABC是等边三角形，根据等边三角形的三条边都相等求出BC，再根据等边三角形的性质求出BC边上的高，然后利用菱形的面积公式列式计算即可得解．
解答 解：如图，∵菱形的一个内角为120°，
∴∠B=180°-120°=60°，
又∵菱形的边AB=BC，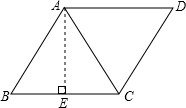
∴△ABC是等边三角形，
∴BC=AC=6，
过点A作AE⊥BC于E，则AE=$\frac{\sqrt{3}}{2}$×6=3$\sqrt{3}$，
∴菱形的面积=BC•AE=6×3$\sqrt{3}$=18$\sqrt{3}$．
故答案为：6，18$\sqrt{3}$．
点评 本题考查了菱形的性质，主要利用了菱形的邻角互补，四条边都相等的性质，等边三角形的判定与性质，作出图形更形象直观．
练习册系列答案
相关题目
6．
如图，甲图中阴影部分的面积是S1，乙图中阴影部分的面积是S2，则下列判断正确的是（ ）
如图，甲图中阴影部分的面积是S1，乙图中阴影部分的面积是S2，则下列判断正确的是（ ）| A． | S1＜S2 | B． | 1＜$\frac{{S}_{2}}{{S}_{1}}$＜2 | C． | S1=S2 | D． | 1＜$\frac{{S}_{1}}{{S}_{2}}$＜2 |
3．某超市经销甲、乙两种商品，第一季度销售这两种商品共获利12000元，且1月，2月，3月的总利润比为8：7：9，甲、乙两种商品的成本与售价如表所示：
请根据以上信息，解答下列问题：
（1）1月份的总利润为4000元；2月份的总利润为3500元；
（2）已知2月份甲商品的销售量比1月份增加了10%，乙商品的销售价比1月份减少了20%，请分别求出1月份甲、乙两种商品的销售量；
（3）已知3月份该商店销售甲商品的数列不到100个，销售乙商品的数量不到90个，请分别求出3月份甲乙两种商品的销售量．
| 商品 | 成本价（元/个） | 销售价（元/个） |
| 甲 | 20 | 40 |
| 乙 | 30 | 60 |
（1）1月份的总利润为4000元；2月份的总利润为3500元；
（2）已知2月份甲商品的销售量比1月份增加了10%，乙商品的销售价比1月份减少了20%，请分别求出1月份甲、乙两种商品的销售量；
（3）已知3月份该商店销售甲商品的数列不到100个，销售乙商品的数量不到90个，请分别求出3月份甲乙两种商品的销售量．