��Ŀ����
10�� ��ͼ��?ABCD�Ķ���OΪ����ԭ�㣬��A��x���������ϣ���COA=60�㣬OA=10��OC=4��������������ͼ���ڵ�һ�����ڹ���C��
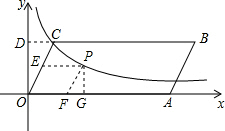
��ͼ��?ABCD�Ķ���OΪ����ԭ�㣬��A��x���������ϣ���COA=60�㣬OA=10��OC=4��������������ͼ���ڵ�һ�����ڹ���C����1�����B�����ꣻ
��2�����������Ľ���ʽ��
��3������P�ڷ���������λ�ڵ�һ����ͼ���ϣ�����P��PE��x�ύ��OC�ڵ�E����PF��OC��x���ڵ�F������ͼ�Σ��ı���OEPF�п���Ϊ���������ܣ��������P�����ꣻ�����ܣ���˵�����ɣ���ע����С��Ľ���ø��ű�ʾ��
���� ��1���ӳ�BC��y���ڵ�D�����ݡ�COA=60�㣬OA=10��OC=4��֪CD=$\frac{1}{2}$OC=2���ʿɵó�B�����ꣻ
��2�����C�����꣬���ô���ϵ������������������Ľ���ʽ���ɣ�
��3����������ı���OEPF�п���Ϊ���Σ�����P��PG��x���ڵ�G������PE��x�ᣬPF��OC��֪�ı���OEPF��ƽ���ı��Σ���OE=PE=2x���ɡ�COA=60���֪FG=x��PG=$\sqrt{3}$x����P��3x��$\sqrt{3}$x�������ɵ�P�ڷ�����������ͼ�������x��ֵ���ɣ�
���  �⣺��1���ӳ�BC��y���ڵ�D��
�⣺��1���ӳ�BC��y���ڵ�D��
�ߡ�COA=60�㣬OA=10��OC=4��
��CD=$\frac{1}{2}$OC=2��
��B��12��2$\sqrt{3}$����
��2����OC=4��CD=2��
��OD=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$��
��C��2��2$\sqrt{3}$����
�෴���������Ľ���ʽΪy=$\frac{4\sqrt{3}}{x}$��
��3���ܣ�
��������ı���OEPF�п���Ϊ���Σ�����P��PG��x���ڵ�G��
��PE��x�ᣬPF��OC��
���ı���OEPF��ƽ���ı��Σ�
��OE=PE=2a��
�ߡ�COA=60�㣬
��FG=a��PG=$\sqrt{3}$a��
��P��3a��$\sqrt{3}$a����
�ߵ�P�ڷ���������y=$\frac{4\sqrt{3}}{x}$��ͼ���ϣ�
��$\sqrt{3}$a=$\frac{4\sqrt{3}}{3a}$��
���a=2��
��P��6��2$\sqrt{3}$����
���� ���⿼����Ƿ����������ۺ��⣬�漰������������ͼ���ϵ�������ص㣬���ε��ж������ʵ�֪ʶ�������������������ߣ��������ν������ǽ�����Ĺؼ���

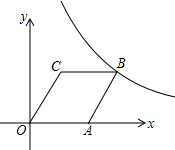 ��ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���O�Ͷ���A����x���ϣ��ҵ�B��8��4���ڷ���������y=$\frac{k}{x}$��x��0����ͼ���ϣ�
��ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���O�Ͷ���A����x���ϣ��ҵ�B��8��4���ڷ���������y=$\frac{k}{x}$��x��0����ͼ���ϣ�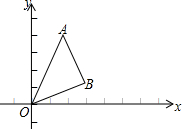 ��ͼ����ƽ��ֱ������ϵ�У���A������Ϊ��2��4������B������Ϊ��3��1��������AOB������ƽ��1����λ���ȣ�������ƽ��1����λ���ȣ�����A��O��B�Ķ�Ӧ��ֱ�ΪD��E��F
��ͼ����ƽ��ֱ������ϵ�У���A������Ϊ��2��4������B������Ϊ��3��1��������AOB������ƽ��1����λ���ȣ�������ƽ��1����λ���ȣ�����A��O��B�Ķ�Ӧ��ֱ�ΪD��E��F ��ͼ��ÿ��С�����εı߳���1��������ͼ�л���һ�������5�������Σ�
��ͼ��ÿ��С�����εı߳���1��������ͼ�л���һ�������5�������Σ�