题目内容
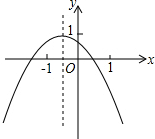 如图所示的二次函数图象,以下四个结论:
如图所示的二次函数图象,以下四个结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0.
你认为正确的有( )
| A、2个 | B、4个 | C、3个 | D、1个 |
考点:二次函数图象与系数的关系
专题:
分析:根据对称轴及抛物线与坐标轴交点情况进行推理,进而对所得结论进行判断.;①根据图象与x轴的交点的个数,解根的判别式b2-4ac与0的大小,②根据图象与y轴交点坐标得出即可,③将对称轴方程x=-
<0变形解答.④取x=1,即可得y=a+b+c的符号.
| b |
| 2a |
解答:解:①图象与x轴有2个交点,依据根的判别式可知b2-4ac>0,故此选项正确;
②∵图象与y轴交点坐标在y轴上方,但在1的下方,
∴1>c>0,故此选项错误;
③∵对称轴方程-1<-
<0,
∴1>
>0;
∵a<0,
∴b>2a,
∴2a-b<0.故此选项正确;
④与图象知,当x=1时,y<0,即a+b+c<0.故此选项正确;
综上所述,正确的说法有①、③、④,共有3个.
故选:C.
②∵图象与y轴交点坐标在y轴上方,但在1的下方,
∴1>c>0,故此选项错误;
③∵对称轴方程-1<-
| b |
| 2a |
∴1>
| b |
| 2a |
∵a<0,
∴b>2a,
∴2a-b<0.故此选项正确;
④与图象知,当x=1时,y<0,即a+b+c<0.故此选项正确;
综上所述,正确的说法有①、③、④,共有3个.
故选:C.
点评:此题考查了二次函数的性质以及图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用,熟练掌握其性质利用数形结合是解题关键.

练习册系列答案
相关题目
“SHERO”五个字母中既是轴对称图形又是中心对称图形是( )
| A、S,H | B、E,R |
| C、H,O | D、S,O |
两圆的半径分别为3和7,圆心距为6,则两圆的交点个数为( )
| A、1个 | B、2个 |
| C、0个 | D、以上都不对 |
一个圆锥的侧面展开图是一个圆心角为216°,面积为60π的扇形,则这个圆锥的高是( )
| A、8 | B、10 | C、12 | D、14 |
已知在Rt△ABC中,∠C=90°,AB=13,AC=12,则∠B的余弦值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,已知∠A=4∠B=104°,则∠C的度数是( )
| A、50° | B、45° |
| C、40° | D、30° |
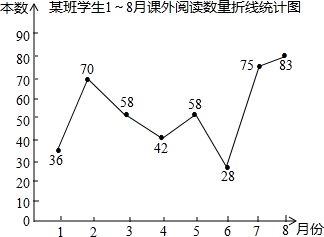 九(1)班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,与上月比较阅读数量变化率最大的月份是( )
九(1)班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,与上月比较阅读数量变化率最大的月份是( )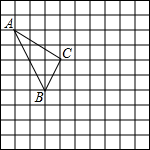 在如图的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,4),(-1,2).
在如图的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,4),(-1,2).