题目内容
20.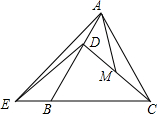 如图,等边△ABC中,点D在边AB上,E在CB的延长线上,已知CD=ED,M是CD中点,AM=2$\sqrt{2}$,则AE=4$\sqrt{2}$.
如图,等边△ABC中,点D在边AB上,E在CB的延长线上,已知CD=ED,M是CD中点,AM=2$\sqrt{2}$,则AE=4$\sqrt{2}$.
分析 由于只告诉了AM的长度,说明AE的长度与AM必然有密切关系,通过观察,猜想它们有二倍关系,又由于M是中点,于是延长AM至F,使MF=AM,连接CF、EM、EF、DF,DF交BC于H,则只需说明三角形AEF是等边三角形即可,容易得到CF=CH=AD,于易证△ABE≌△ACF,然后可轻松得出三角形AEF是等边三角形的结论,答案不言而喻.
解答 解:延长AM至F,使MF=AM,连接CF、EM、EF、DF,DF交BC于H,如图,
∵DM=CM,
∴ACFD是平行四边形,
∴CF=AD,
∵△ABC是等边三角形,
∴AD=CH,
∴△DBH是等边三角形,
∴DB=DH=BH,∠DBH=∠DHB=60°,
∴∠DBE=∠DHC=120°,
∵DE=DC,
∴∠DEB=∠DCH,
∴△DBE≌△DHC,
∴BE=CH=CF,
在△ABE和△ACF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠ABE=∠ACF}\\{BE=CF}\end{array}\right.$,
∴△ABE≌△ACF(SAS),
∴AE=AF,∠EAB=∠FAC,
∴∠EAF=∠BAC=60°,
∴△AEF是等边三角形,
∴EM⊥AM,
∴AE=2AM=4$\sqrt{2}$,
故答案为4$\sqrt{2}$.
点评 本题主要考查了等边三角形的判定与性质、等腰三角形的性质、全等三角形的判定与性质、平行四边形的判定与性质等知识点,难度较大.本题看似简单,却不好下手,在这种情况,抓住“题眼”是关键,本题的“题眼”就是“中点”,因此,熟悉“中点”的用法就特别重要.

练习册系列答案
相关题目
8.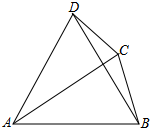 如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=78°,∠BDC=24°,则∠DBC=( )
如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=78°,∠BDC=24°,则∠DBC=( )
 如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=78°,∠BDC=24°,则∠DBC=( )
如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=78°,∠BDC=24°,则∠DBC=( )| A. | 18° | B. | 20° | C. | 25° | D. | 15° |
15. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )
 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )| A. | 8 | B. | 10 | C. | 2$\sqrt{21}$或8 | D. | 2$\sqrt{21}$或10 |
12.一个三角形的两边长为4和6,第三边的边长是方程(x-2)(x-5)=0的根,则这个三角形的周长为( )
| A. | 12 | B. | 15 | C. | 12或15 | D. | 以上都不对 |
 如图所示,地面上的电线杆AB、CD都与地面垂直,那么电线杆AB和CD平行吗?为什么?
如图所示,地面上的电线杆AB、CD都与地面垂直,那么电线杆AB和CD平行吗?为什么?