题目内容
4.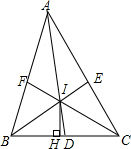 如图,在△ABC中,三角形内角平分线AD,BE,CF相交于点I,IH⊥BC于点H,求证:∠BID=∠HIC.
如图,在△ABC中,三角形内角平分线AD,BE,CF相交于点I,IH⊥BC于点H,求证:∠BID=∠HIC.
分析 根据角平分线的定义、三角形内角和定理可知∠BAD+∠ABI+∠HCI=90°.又因为∠BAD+∠ABI=∠BID,90°-∠HCI=∠CIH,所以∠BID=∠CIH.
解答 证明:∵AD,BE,CF为三角形ABC的角平分线,
∴∠BAD=$\frac{1}{2}$∠BAC,∠ABI=$\frac{1}{2}$∠ABC,∠HCI=$\frac{1}{2}$∠ACB.
∴∠BAD+∠ABI+∠HCI=$\frac{1}{2}$∠BAC+$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=$\frac{1}{2}$(∠BAC+∠ABC+∠ACB)=$\frac{1}{2}$×180°=90°.
∴∠BAD+∠ABI=90°-∠HCI.
又∵∠BAD+∠ABI=∠BID,90°-∠HCI=∠CIH
2(∠BAD+∠ABI+∠HCI)=180°,
∴∠BAD+∠ABI+∠HCI=90°,
∴∠BID=∠CIH.
点评 本题考查了角平分线的定义及三角形内角和定理,掌握三角形三个内角的和为180°是解决问题的关键.

练习册系列答案
相关题目
16.已知2x-3的立方根是5,则x的平方根是( )
| A. | 64 | B. | 8 | C. | ±8 | D. | ±64 |
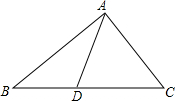 如图,点D是△ABC的边BC上任意一点,则AB+BC+AC>2AD.请说明理由.
如图,点D是△ABC的边BC上任意一点,则AB+BC+AC>2AD.请说明理由.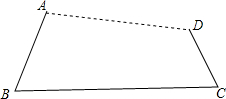 如图,用钉子把木棒AB、BC和CD分别在端点B、C处连接起来,用橡皮筋把AD连接起来
如图,用钉子把木棒AB、BC和CD分别在端点B、C处连接起来,用橡皮筋把AD连接起来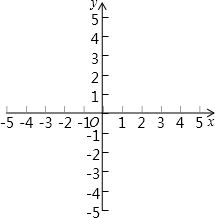 如图,在同一平面直角坐标系中画出函数y=$\frac{1}{2}$x2和y=2x2的图象
如图,在同一平面直角坐标系中画出函数y=$\frac{1}{2}$x2和y=2x2的图象