题目内容
3.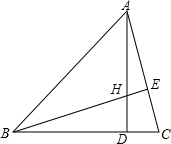 如图,△ABC中,H是高AD、BE的交点,且BH=AC,则∠ABC=45°.
如图,△ABC中,H是高AD、BE的交点,且BH=AC,则∠ABC=45°.
分析 求出△ADC≌△BDH,推出AD=BD,根据等腰三角形性质得出∠ABD=∠BAD,根据三角形内角和定理求出即可.
解答 解:∵AD、BE是△ABC的高,
∴∠ADC=∠BDH=90°,∠∠BEC=90°,
∴∠C+∠CAD=90°,∠C+∠HBD=90°,
∴∠CAD=∠HBD,
在△HBD和△CAD中,$\left\{\begin{array}{l}{∠HBD=∠CAD}\\{∠BDH=∠ADC=90°}\\{BH=AC}\end{array}\right.$,
∴△HBD≌△CAD(AAS),
∴BD=AD,
∵∠ADB=90°,
∴∠ABC=∠BAD=45°,
故答案为:45°.
点评 本题考查了等腰三角形的性质,三角形内角和定理,全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
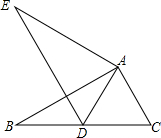 如图,已知△ABC≌△AED,∠E=∠B,∠C=∠ADE,若∠BAD=$\frac{1}{3}$∠EAD=30°,求∠DAC的度数.
如图,已知△ABC≌△AED,∠E=∠B,∠C=∠ADE,若∠BAD=$\frac{1}{3}$∠EAD=30°,求∠DAC的度数.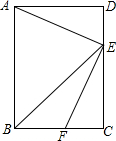 如图,在矩形中,BE平分∠ABC,交CD于点E,点F在边BC上.
如图,在矩形中,BE平分∠ABC,交CD于点E,点F在边BC上.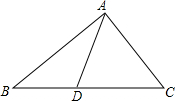 如图,点D是△ABC的边BC上任意一点,则AB+BC+AC>2AD.请说明理由.
如图,点D是△ABC的边BC上任意一点,则AB+BC+AC>2AD.请说明理由.