题目内容
12.如图1,两个等边△ABD,△CBD的边长均为2,将△ABD沿AC方向向右平移k个单位到△A′B′D′的位置,得到图2,则下列说法:①阴影部分的周长为4;②当k=1时,图中阴影部分为正六边形;③若阴影部分和空白部分的面积相等,则k=$\frac{\sqrt{3}}{2}$.其中正确的说法是( )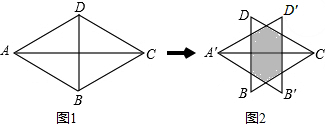
| A. | ① | B. | ①② | C. | ②③ | D. | ①②③ |
分析 根据两个等边△ABD,△CBD的边长均为2,将△ABD沿AC方向向右平移到△A′B′D′的位置,得出线段之间的相等关系,进而得出OM+MN+NR+GR+EG+OE=A′D′+CD,即可得出答案.
解答  解:∵两个等边△ABD,△CBD的边长均为2,将△ABD沿AC方向向右平移到△A′B′D′的位置,
解:∵两个等边△ABD,△CBD的边长均为2,将△ABD沿AC方向向右平移到△A′B′D′的位置,
∴A′M=A′N=MN,MO=DM=DO,OD′=D′E=OE,EG=EC=GC,B′G=RG=RB′,
∴OM+MN+NR+GR+EG+OE=A′D′+CD=2+2=4,故①正确;
∵k=1,
∴A′F=1,
∴A′M=A′F÷cos30°=$\frac{2\sqrt{3}}{3}$,MN=$\frac{2\sqrt{3}}{3}$,
∴MO=$\frac{1}{2}$(2-$\frac{2\sqrt{3}}{3}$)=1-$\frac{\sqrt{3}}{3}$,
∴MO≠MN,
∴阴影部分不是正六边形,故此选项错误;
当k=$\frac{\sqrt{3}}{2}$时,阴影部分和空白部分的面积不相等,故此选项错误.
故选:A.
点评 此题主要考查了菱形的性质、平移的性质以及等边三角形的性质,根据题意得出A′M=A′N=MN,MO=DM=DO,OD′=D′E=OE,EG=EC=GC,B′G=RG=RB′是解决问题的关键.

练习册系列答案
相关题目
4.甲乙两战士各射靶10次,总成绩都是99.68环,甲的方差是0.28,乙的方差是0.21,则下列说法中,正确的是( )
| A. | 乙的成绩比甲的成绩稳定 | B. | 甲的成绩比乙的成绩稳定 | ||
| C. | 甲和乙成绩的稳定性相同 | D. | 无法确定甲乙成绩的稳定性 |
2.父子二人在周长为400m的环形跑道上练习跑步,同时同地背向起跑,20秒后两人第一次相遇,已知父速为子速的1.5倍.设儿子每秒跑xm,列方程为( )
| A. | 1.5x-x=1 | B. | 1.5x+x=1 | C. | 20(1.5x+x)=400 | D. | 20(1.5x-x)=400 |
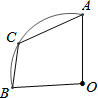 如图,在扇形OAB中,∠AOB=90°,点C在$\widehat{AB}$上,若BC=4,AC=5$\sqrt{2}$,则扇形OAB的面积为$\frac{53π}{4}$.
如图,在扇形OAB中,∠AOB=90°,点C在$\widehat{AB}$上,若BC=4,AC=5$\sqrt{2}$,则扇形OAB的面积为$\frac{53π}{4}$. 已知,如图△ABC,
已知,如图△ABC,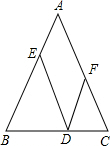 如图,在△ABC中,AB=AC,点D在BC上,DE∥AC交AB于点E,DF∥AB交AC于点F,试说明线段DE,DF,AB三者之间的数量关系.
如图,在△ABC中,AB=AC,点D在BC上,DE∥AC交AB于点E,DF∥AB交AC于点F,试说明线段DE,DF,AB三者之间的数量关系.