题目内容
17. 已知,如图△ABC,
已知,如图△ABC,(1)求作△ABC的外接圆⊙O.(用尺规作图,保留必要的画图痕迹);
(2)若AB和AC是⊙O的内接正五边形的两条边,请求出∠ABC的度数,并找出BC边上的黄金分割点P.(一个即可)
分析 (1)利用三角形外接圆的作法得出圆心的位置进而得出即可;
(2)利用正五边形的性质以及黄金分割点的定义得出即可.
解答  解:(1)如图所示:⊙O即为所求;
解:(1)如图所示:⊙O即为所求;
(2)由正五边形的性质可得:∠BAC=(5-2)×180÷5=108°,
∵AB=AC,∴∠ABC=∠ACB,
∴∠ABC=(180-108)÷2=36°,
在BC上截取BP=BA或者CP=BA,则点P即为所求的点.
点评 此题主要考查了复杂作图以及黄金分割点的作图,正确掌握三角形外接圆的作法是解题关键.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
7.有下列说法:①如果两直线都与第三条直线平行,那么这两条直线也互相平行.②直线外一点到这条直线的垂线段,叫做点到直线的距离.③△ABC在平移过程中周长不变.④三角形的中线、角平分线、高线都在三角形内部.其中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.给出四个数:-1、0、$\sqrt{2}$、3.14,其中为无理数的是( )
| A. | -1 | B. | 0 | C. | $\sqrt{2}$ | D. | 3.14 |
 如图,AB∥CD,BC平分∠ECD交AB于点B,若∠EAB=60°,则∠BCD=30°.
如图,AB∥CD,BC平分∠ECD交AB于点B,若∠EAB=60°,则∠BCD=30°.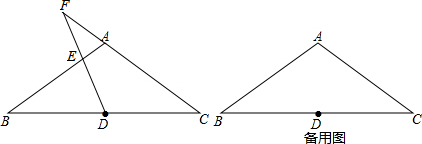
 如图,在⊙O中,AB为⊙O的直径,弦CD⊥AB,垂足为E.若∠BAD=30°,且BE=2,则CD=4$\sqrt{3}$.
如图,在⊙O中,AB为⊙O的直径,弦CD⊥AB,垂足为E.若∠BAD=30°,且BE=2,则CD=4$\sqrt{3}$.