题目内容
1.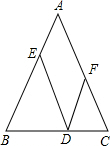 如图,在△ABC中,AB=AC,点D在BC上,DE∥AC交AB于点E,DF∥AB交AC于点F,试说明线段DE,DF,AB三者之间的数量关系.
如图,在△ABC中,AB=AC,点D在BC上,DE∥AC交AB于点E,DF∥AB交AC于点F,试说明线段DE,DF,AB三者之间的数量关系.
分析 根据等腰三角形的性质,可得∠B与∠C的关系,根据平行线的性质,可得∠C与∠BDE的关系,根据等腰三角形的判定,可得BE与DE的关系,根据平行四边形的判定与性质,可得DF与AE的关系.
解答 解:DE+DF=AB,理由如下:
∵AB=AC,
∴∠B=∠C.
∵DE∥AC交AB于点E,
∴∠C=∠BDE,
∴∠B=∠BDE,
∴BE=DE.
∵DE∥AC交AB于点E,DF∥AB交AC于点F,
∴四边形AEDF是平行四边形,
∴AE=DF.
∵AE+BE=AB,
∴DE+DF=AB.
点评 本题考查了等腰三角形的判定与性质,利用等腰三角形的判定与性质、平行四边形的判定与性质,得出BE与DE的关系、DF与AE的关系是解题关键.

练习册系列答案
相关题目
13.下列运算正确的是( )
| A. | 3-1=-3 | B. | $\sqrt{9}$=±3 | C. | (ab2)3=a3b6 | D. | a2+a3=a5 |
10. 如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=55°,则∠BAC的大小等于( )
如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=55°,则∠BAC的大小等于( )
 如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=55°,则∠BAC的大小等于( )
如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=55°,则∠BAC的大小等于( )| A. | 55° | B. | 45° | C. | 35° | D. | 30° |
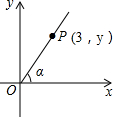 如图,直角坐标系中,P(3,y)是第一象限内的点,且$tanα=\frac{4}{3}$,求sinα.
如图,直角坐标系中,P(3,y)是第一象限内的点,且$tanα=\frac{4}{3}$,求sinα.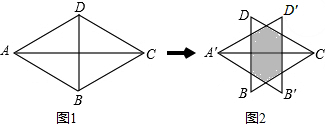
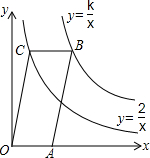 如图,已知点A在x轴上,?OABC的顶点B在反比例函数y=$\frac{k}{x}$的图象上,顶点C在反比例函数y=$\frac{2}{x}$的图象上,?OABC的面积等于4.
如图,已知点A在x轴上,?OABC的顶点B在反比例函数y=$\frac{k}{x}$的图象上,顶点C在反比例函数y=$\frac{2}{x}$的图象上,?OABC的面积等于4. 如图,在⊙O中,AB为⊙O的直径,弦CD⊥AB,垂足为E.若∠BAD=30°,且BE=2,则CD=4$\sqrt{3}$.
如图,在⊙O中,AB为⊙O的直径,弦CD⊥AB,垂足为E.若∠BAD=30°,且BE=2,则CD=4$\sqrt{3}$.