题目内容
6.若(ax-b)(3x+4)=bx2+cx+72,则a+b+c的值为6.分析 已知等式左边利用多项式乘以多项式法则计算,利用多项式相等的条件求出a,b,c的值,即可求出a+b+c的值.
解答 解:∵(ax-b)(3x+4)=3ax2+(4a-3b)x-4b=bx2+cx+72,
∴3a=b,4a-3b=c,-4b=72,
解得:a=-6,b=-18,c=30,
则a+b+c=-6-18+30=6.
故答案为:6
点评 此题考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.已知5个正数,a,b,c,d,e的平均数是x,且a<b<c<d<e,则新一组数据a,b,0,c,d,e的平均数和中位数分别是( )
| A. | x,$\frac{c}{2}$ | B. | x,$\frac{b+c}{2}$ | C. | $\frac{5}{6}$x,$\frac{c}{2}$ | D. | $\frac{5}{6}x$,$\frac{b+c}{2}$ |
17.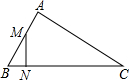 如图,△ABC中,M是AB的中点,N在BC上,BC=2AB,∠BMN=∠C,则△BMN∽△BCA,相似比为$\frac{1}{4}$,$\frac{BN}{NC}$=$\frac{1}{7}$.
如图,△ABC中,M是AB的中点,N在BC上,BC=2AB,∠BMN=∠C,则△BMN∽△BCA,相似比为$\frac{1}{4}$,$\frac{BN}{NC}$=$\frac{1}{7}$.
 如图,△ABC中,M是AB的中点,N在BC上,BC=2AB,∠BMN=∠C,则△BMN∽△BCA,相似比为$\frac{1}{4}$,$\frac{BN}{NC}$=$\frac{1}{7}$.
如图,△ABC中,M是AB的中点,N在BC上,BC=2AB,∠BMN=∠C,则△BMN∽△BCA,相似比为$\frac{1}{4}$,$\frac{BN}{NC}$=$\frac{1}{7}$.
16.下列运算正确的是( )
| A. | x4•x4=x16 | B. | a2+a2=a4 | C. | (a6)2÷(a4)3=1 | D. | (a+b)2=a2+b2 |
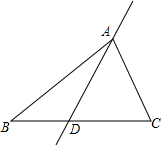 如图,已知△ABC,点D在BC边上,过点A作直线AD.
如图,已知△ABC,点D在BC边上,过点A作直线AD.