题目内容
2.解不等式$\left\{\begin{array}{l}{\frac{1-2x}{3}-\frac{4-3x}{6}≥\frac{x-2}{2}}\\{2x-7≤3(x-1)}\end{array}\right.$,并把它的解集在数轴上表示出来.分析 根据不等式的性质求出不等式的解集,根据找不等式组解集的规律找出即可.
解答 解:原式可化为$\left\{\begin{array}{l}{2(1-2x)-(4-3x)≥3(x-2)①}\\{2x-7≤3(x-1)②}\end{array}\right.$,
由①得:x≤1,
由②得:x≥-4,
∴不等式组的解集是-4≤x≤1.
把不等式组的解集在数轴上表示为:
点评 本题主要考查对解一元一次不等式(组),不等式的性质,在数轴上表示不等式的解集等知识点的理解和掌握,能根据不等式的解集找出不等式组的解集是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

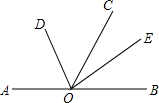 如图,直线AB上有点O,作射线OC,作OD平分∠AOC,OE平分∠BOC,求∠DOE的度数.
如图,直线AB上有点O,作射线OC,作OD平分∠AOC,OE平分∠BOC,求∠DOE的度数.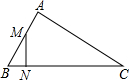 如图,△ABC中,M是AB的中点,N在BC上,BC=2AB,∠BMN=∠C,则△BMN∽△BCA,相似比为$\frac{1}{4}$,$\frac{BN}{NC}$=$\frac{1}{7}$.
如图,△ABC中,M是AB的中点,N在BC上,BC=2AB,∠BMN=∠C,则△BMN∽△BCA,相似比为$\frac{1}{4}$,$\frac{BN}{NC}$=$\frac{1}{7}$.