题目内容
 △ABC中,AB=AC,AD⊥BC于D,以AC为边在△ABC外作等边△ACE,连BE交AD于M;
△ABC中,AB=AC,AD⊥BC于D,以AC为边在△ABC外作等边△ACE,连BE交AD于M;(1)求证:MD=
| 1 |
| 2 |
(2)若AM=5,MD=2,求ME.
考点:相似三角形的判定与性质,角平分线的性质,等边三角形的性质
专题:
分析:(1)利用条件证明∠BMD=60°即可,利用等边三角形和等腰三角形的性质可求得∠BMD=∠AMG=∠GMC=∠EAG=60°,可证得结论;
(2)利用角平分线的性质和△MCE∽△CGE,可得到线段之间的关系,代入可求得ME.
(2)利用角平分线的性质和△MCE∽△CGE,可得到线段之间的关系,代入可求得ME.
解答: 证明:(1)如图,连接CM,
证明:(1)如图,连接CM,
∵AB=AC,AD⊥BC,
∴AD为BC垂直平分线,
∴BM=CM,
∴∠ABC=∠ACB,∠MBD=∠MCD,
∴∠ABM=∠ACM,
∵AB=AE,
∴∠ABM=∠AEB,
∴∠ACM=∠AEB,
又∵∠AGE=∠CGM,
∴∠EMC=∠EAC=60°,
又∵∠EMC=∠MBC+∠MCB,
∴∠MBC=30°,
∴MD=
BM;
(2)∵∠AME=∠BMD=60°=∠CME,
∴MG是△AMC的角平分线,
∴
=
=
,
∴CG=
AC,
∵△MCE∽△CGE,
∴
=
,
∴ME=
=
=9.
 证明:(1)如图,连接CM,
证明:(1)如图,连接CM,∵AB=AC,AD⊥BC,
∴AD为BC垂直平分线,
∴BM=CM,
∴∠ABC=∠ACB,∠MBD=∠MCD,
∴∠ABM=∠ACM,
∵AB=AE,
∴∠ABM=∠AEB,
∴∠ACM=∠AEB,
又∵∠AGE=∠CGM,
∴∠EMC=∠EAC=60°,
又∵∠EMC=∠MBC+∠MCB,
∴∠MBC=30°,
∴MD=
| 1 |
| 2 |
(2)∵∠AME=∠BMD=60°=∠CME,
∴MG是△AMC的角平分线,
∴
| AG |
| CG |
| AM |
| MC |
| 5 |
| 4 |
∴CG=
| 4 |
| 9 |
∵△MCE∽△CGE,
∴
| CG |
| CM |
| CE |
| ME |
∴ME=
| CE•CM |
| CG |
| 4AC | ||
|
点评:本题主要考查相似三角形的判定和性质及等腰、等边三角形的性质,在(1)中证得∠BMD=60°是解题的关键,在(2)中利用角平分线的性质定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列命题是真命题的是( )
| A、由a>b可以推出a2>b2 |
| B、由a2>b2可以推出a>b |
| C、相等的角是对顶角 |
| D、两条对角线互相垂直的平行四边形是菱形 |
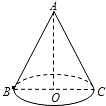 如图,圆锥的轴截面△ABC是一个以圆锥的底面直径为底边,圆锥的母线为腰的等腰三角形,若圆锥的底面直径BC=4cm,母线AB=6cm,则由点B出发,经过圆锥的侧面到达母线AC的最短路程是
如图,圆锥的轴截面△ABC是一个以圆锥的底面直径为底边,圆锥的母线为腰的等腰三角形,若圆锥的底面直径BC=4cm,母线AB=6cm,则由点B出发,经过圆锥的侧面到达母线AC的最短路程是
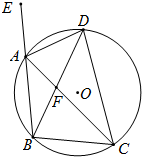 如图,等腰△ABC内接于⊙O,AB=BC,它的外角∠EAC的平分线交⊙O于D点,DB交AC于F.
如图,等腰△ABC内接于⊙O,AB=BC,它的外角∠EAC的平分线交⊙O于D点,DB交AC于F. 如图,已知∠1=∠2,∠3=∠4,若∠AOE=128°,求∠BOD的度数.
如图,已知∠1=∠2,∠3=∠4,若∠AOE=128°,求∠BOD的度数. 如图所示,D是BA延长线上的点,E是BC延长线上的点,连接CD,∠1=∠2,求证:∠BAC>∠B.
如图所示,D是BA延长线上的点,E是BC延长线上的点,连接CD,∠1=∠2,求证:∠BAC>∠B.