题目内容
 如图,在一个矩形纸片ABCD剪上减去一个正方形ABEF,所余下的矩形ECDF于原矩形ABCD相似,那么原矩形中较长的边BC与较短的边AB的比是多少?
如图,在一个矩形纸片ABCD剪上减去一个正方形ABEF,所余下的矩形ECDF于原矩形ABCD相似,那么原矩形中较长的边BC与较短的边AB的比是多少?考点:相似多边形的性质
专题:
分析:由题意可得矩形CDFE与矩形ABCD相似,则可得
=
,继而可得AB2=BC×(BC-AB),则可求得原矩形中较长的边BC与较短的边AB的比.
| BC |
| CD |
| CD |
| CE |
解答:解:∵矩形CDFE与矩形ABCD相似,
∴
=
,
∴CD2=BC×CE=BC(BC-CD),
即AB2=BC×(BC-AB),
∴AB2+AB•BC-BC2=0,
方程两边同除以AB2得:1+
-(
)2=0,
解得:
=
.
∴原矩形中较长的边BC与较短的边AB的比是:
.
∴
| BC |
| CD |
| CD |
| CE |
∴CD2=BC×CE=BC(BC-CD),
即AB2=BC×(BC-AB),
∴AB2+AB•BC-BC2=0,
方程两边同除以AB2得:1+
| BC |
| AB |
| BC |
| AB |
解得:
| BC |
| AB |
| ||
| 2 |
∴原矩形中较长的边BC与较短的边AB的比是:
| ||
| 2 |
点评:此题考查了相似多边形的性质.此题难度适中,注意掌握相似多边形的对应边的比相等.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
下列命题是真命题的是( )
| A、由a>b可以推出a2>b2 |
| B、由a2>b2可以推出a>b |
| C、相等的角是对顶角 |
| D、两条对角线互相垂直的平行四边形是菱形 |
圆锥的高为4cm,底面圆直径长6cm,则该圆锥的侧面积等于( )cm2.
| A、24π | B、15π |
| C、30π | D、12π |
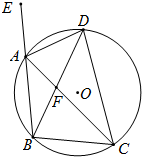 如图,等腰△ABC内接于⊙O,AB=BC,它的外角∠EAC的平分线交⊙O于D点,DB交AC于F.
如图,等腰△ABC内接于⊙O,AB=BC,它的外角∠EAC的平分线交⊙O于D点,DB交AC于F. 如图,在△ABC中,BC=4,AC=13,AB=15,求S△ABC.
如图,在△ABC中,BC=4,AC=13,AB=15,求S△ABC.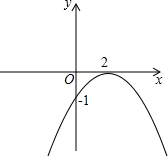 如图是y=a(x+m)2的图象
如图是y=a(x+m)2的图象 如图所示,D是BA延长线上的点,E是BC延长线上的点,连接CD,∠1=∠2,求证:∠BAC>∠B.
如图所示,D是BA延长线上的点,E是BC延长线上的点,连接CD,∠1=∠2,求证:∠BAC>∠B. 如图所示,在四边形ABCD中,∠A-∠C=∠D-∠B,求证:AD∥BC.
如图所示,在四边形ABCD中,∠A-∠C=∠D-∠B,求证:AD∥BC.