题目内容
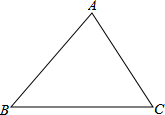 如图,在△ABC中,∠B=45°,∠BAC=75°,AC=8.求AB和BC的长.
如图,在△ABC中,∠B=45°,∠BAC=75°,AC=8.求AB和BC的长.考点:解直角三角形
专题:
分析:作AD⊥BC,根据特殊角三角函数值可以求得CD,AD的长,即可求得BC的长,根据△ABD为等腰直角三角形可求得AB的长,即可解题.
解答:解:作AD⊥BC,

∵∠B=45°,∠BAC=75°,
∴∠BAD=45°,∠CAD=30°,
∴AC=2CD,AD=BD,
∴CD=4,BD=AD=4
,
∴BC=BD+CD=4
+4,
AB=
AD=4
.

∵∠B=45°,∠BAC=75°,
∴∠BAD=45°,∠CAD=30°,
∴AC=2CD,AD=BD,
∴CD=4,BD=AD=4
| 3 |
∴BC=BD+CD=4
| 3 |
AB=
| 2 |
| 6 |
点评:本题考查了特殊角的三角函数值,考查了直角三角形中三角函数的运用,本题中求AD的长是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
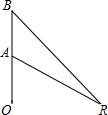 如图,一枚运载火箭从地面O处发射,当火箭到达点A处时,地面R处的雷达站测得AR的距离是6km,仰角为30°.5s后,火箭到达点B处,此时BR的距离为6.25km,仰角为45°.求火箭从A处到B处的平均速度(结果精确到1m/s)
如图,一枚运载火箭从地面O处发射,当火箭到达点A处时,地面R处的雷达站测得AR的距离是6km,仰角为30°.5s后,火箭到达点B处,此时BR的距离为6.25km,仰角为45°.求火箭从A处到B处的平均速度(结果精确到1m/s) 如图,△ABC中,DE∥BC,DF∥AC,求证:△ADE∽△DBF.
如图,△ABC中,DE∥BC,DF∥AC,求证:△ADE∽△DBF. 已知:如图,在△ABC中,AB>AC,AD平分∠BAC,BE垂直AD延长线于E,M是BC中点.求证:EM=
已知:如图,在△ABC中,AB>AC,AD平分∠BAC,BE垂直AD延长线于E,M是BC中点.求证:EM=