题目内容
在直角三角形中,两直角边在斜边上的射影分别为4cm和9cm,则它的较短的直角边的长度是 .
考点:射影定理
专题:计算题
分析:如图,∠BAC=90°,CD⊥B于D,则BD=4cm,CD=9cm,根据射影定理得到AB2=BD•BC=4(4+9),然后根据算术平方根的定义求解.
解答: 解:如图,∠BAC=90°,CD⊥B于D,则BD=4cm,CD=9cm,
解:如图,∠BAC=90°,CD⊥B于D,则BD=4cm,CD=9cm,
所以AB2=BD•BC=4(4+9),
所以AB=2
(cm).
故答案为2
cm.
 解:如图,∠BAC=90°,CD⊥B于D,则BD=4cm,CD=9cm,
解:如图,∠BAC=90°,CD⊥B于D,则BD=4cm,CD=9cm,所以AB2=BD•BC=4(4+9),
所以AB=2
| 13 |
故答案为2
| 13 |
点评:本题考查了射影定理:直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项.每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 已知△ABC中,∠C=90°,点D在AC上,DE⊥AB于点E,且DC=DE,∠A=40°,求∠CBD的度数.
已知△ABC中,∠C=90°,点D在AC上,DE⊥AB于点E,且DC=DE,∠A=40°,求∠CBD的度数.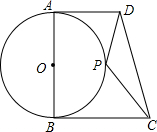 已知:AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=3,AB=4,BC=6,则△PCD的面积的最小值是( )
已知:AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=3,AB=4,BC=6,则△PCD的面积的最小值是( )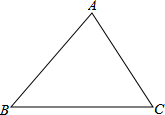 如图,在△ABC中,∠B=45°,∠BAC=75°,AC=8.求AB和BC的长.
如图,在△ABC中,∠B=45°,∠BAC=75°,AC=8.求AB和BC的长.