题目内容
 已知:如图,在△ABC中,AB>AC,AD平分∠BAC,BE垂直AD延长线于E,M是BC中点.求证:EM=
已知:如图,在△ABC中,AB>AC,AD平分∠BAC,BE垂直AD延长线于E,M是BC中点.求证:EM=| 1 |
| 2 |
考点:三角形中位线定理,等腰三角形的判定与性质
专题:证明题
分析:延长BE与AC的延长线交于点F,可证得Rt△AEF≌Rt△AEB,可得AF=AB,则有CF=AB-AC,且E为中点,ME是△BFC的中位线,可得出结论.
解答: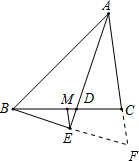 证明:延长BE与AC延长线交于F点,过C作CN∥ME,交BF于点N
证明:延长BE与AC延长线交于F点,过C作CN∥ME,交BF于点N
∵AD平分∠BAC,BE⊥AE
∴∠BAE=∠FAE,∠BEA=∠FEA,
在△AEF和△AEB中,
,
∴△AEF≌△AEB(ASA),
∴BE=EF,AF=AB,且AF=AC+CF,
∴CF=AB-AC,
∵M为BC中点,E为BF中点,
∴ME为△BCF的中位线,
∴EM=
CF=
(AB-AC).
 证明:延长BE与AC延长线交于F点,过C作CN∥ME,交BF于点N
证明:延长BE与AC延长线交于F点,过C作CN∥ME,交BF于点N∵AD平分∠BAC,BE⊥AE
∴∠BAE=∠FAE,∠BEA=∠FEA,
在△AEF和△AEB中,
|
∴△AEF≌△AEB(ASA),
∴BE=EF,AF=AB,且AF=AC+CF,
∴CF=AB-AC,
∵M为BC中点,E为BF中点,
∴ME为△BCF的中位线,
∴EM=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查全等三角形的判定和性质及三角形中位线定理,构造三角形全等把所证结论转化成证明EM=
CF是解题的关键.
| 1 |
| 2 |

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
甲乙两地相距20千米,某人从甲地去乙地,先步行走了8千米,又骑自行车到达乙地,共用了3小时,如果这个人骑自行车的速度是步行速度的3倍,那么他步行的速度是( )
| A、4千米/时 |
| B、6千米/时 |
| C、3千米/时 |
| D、8千米/时 |
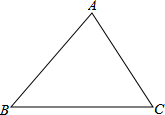 如图,在△ABC中,∠B=45°,∠BAC=75°,AC=8.求AB和BC的长.
如图,在△ABC中,∠B=45°,∠BAC=75°,AC=8.求AB和BC的长.