题目内容
在Rt△ABC中，∠C=90°，CD为斜边上的高，若AC：AB=3：5，则AD：BD= ．
考点：解直角三角形
专题：
分析：画出图形，易证△ACD∽△ABC∽△CBD，即可求得
=CD2，根据勾股定理可求得BC的长度，即可求得CD的长度，即可解题．
| AD |
| BD |
解答：解：画出图形，
∵∠ACB=90°，CD⊥AB，
∴△ACD∽△ABC∽△CBD，
∴
=
，
∴
=CD2，
∵RT△ABC中，AC：AB=3：5，令AC=3，AB=5，
∴BC=4，
∴CD=
=
，
∴
=CD2=
．
故答案为
．
∵∠ACB=90°，CD⊥AB，
∴△ACD∽△ABC∽△CBD，
∴
| AD |
| CD |
| CD |
| BD |
∴
| AD |
| BD |
∵RT△ABC中，AC：AB=3：5，令AC=3，AB=5，
∴BC=4，
∴CD=
| AC•BC |
| AB |
| 12 |
| 5 |
∴
| AD |
| BD |
| 144 |
| 25 |
故答案为
| 144 |
| 25 |
点评：本题考查了直角三角形中勾股定理的运用，考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质，本题中求得
=CD2是解题的关键．
| AD |
| BD |
练习册系列答案
阅读快车系列答案
相关题目
六年级1班有x人，六年级2班比六年级1班人数的
少1人，则六年级2班人数是（ ）
| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，在△ABC中，∠B=45°，∠BAC=75°，AC=8．求AB和BC的长．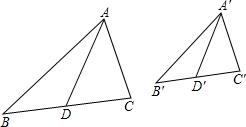
如图，△ABC∽△A′B′C′，AD、A′D′分别是它们的中线，求证：AD：A′D′=AB：A′B′．