题目内容
在△ABC中,∠A=
∠C,∠B
∠C,则此三角形是( )
| 1 |
| 2 |
| 1 |
| 3 |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
考点:三角形内角和定理
专题:
分析:设∠C=6x,则∠A=3x,∠B=2x,再根据三角形内角和定理求出x的值,进而得出结论.
解答:解:∵在△ABC中,∠A=
∠C,∠B=
∠C,
∴设∠C=6x,则∠A=3x,∠B=2x,
∵∠A+∠B+∠C=180°,即3x+2x+6x=180°,解得x=
,
∴∠C=6×
≈98.2°,
∴此三角形是钝角三角形.
故选C.
| 1 |
| 2 |
| 1 |
| 3 |
∴设∠C=6x,则∠A=3x,∠B=2x,
∵∠A+∠B+∠C=180°,即3x+2x+6x=180°,解得x=
| 180° |
| 11 |
∴∠C=6×
| 180° |
| 11 |
∴此三角形是钝角三角形.
故选C.
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
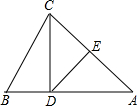 如图,DE⊥AC,垂足为E,CE=AE.若AB=12cm,BC=10cm,则△BCD的周长是( )
如图,DE⊥AC,垂足为E,CE=AE.若AB=12cm,BC=10cm,则△BCD的周长是( )| A、22cm | B、16cm |
| C、23cm | D、25cm |
已知在△ABC和△DEF中,∠B=∠E,∠C=∠F,只要满足下列条件中的( )即有△ABC≌△DEF.
| A、AC=DE |
| B、BC=EF |
| C、AB=DF |
| D、BC=DF |
观察下列式子,正确的是( )
| A、-2(x-3y)=-2x+6y |
| B、a+3>3 |
| C、4÷(2+1)=4÷2+4÷1 |
| D、16y2-7y2=9 |

 如图已知:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D
如图已知:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D