题目内容
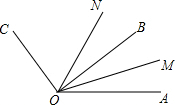 如图,已知∠AOB在∠AOC内部,∠BOC=90°,OM、ON分别是∠AOB,∠AOC的平分线,∠AOB与∠COM互补,求∠BON的度数.
如图,已知∠AOB在∠AOC内部,∠BOC=90°,OM、ON分别是∠AOB,∠AOC的平分线,∠AOB与∠COM互补,求∠BON的度数.考点:余角和补角
专题:
分析:根据补角的性质,可得∠AOB+∠COM=180°,根据角的和差,可得∠AOB+∠BOM=90°,根据角平分线的性质,可得∠BOM=
∠AOB,根据解方程,可得∠AOB的度数,根据角的和差,可得答案.
| 1 |
| 2 |
解答:解:由∠AOB与∠COM互补,得
∠AOB+∠COM=180°.
由角的和差,得∠AOB+BOM+∠COB=180°,
∠AOB+∠BOM=90°.
由OM是∠AOB的平分线,得
∠BOM=
∠AOB,
即∠AOB+
∠AOB=90°.
解得∠AOB=60°.
由角的和差,得∠AOC=∠BOC+∠AOB=90°+60°=150°.
由ON平分∠AOC得,∠AON=
∠AOC=
×150°=75°,
由角的和差,得
∠BON=∠AON-∠AOB=75°-60°=15°.
∠AOB+∠COM=180°.
由角的和差,得∠AOB+BOM+∠COB=180°,
∠AOB+∠BOM=90°.
由OM是∠AOB的平分线,得
∠BOM=
| 1 |
| 2 |
即∠AOB+
| 1 |
| 2 |
解得∠AOB=60°.
由角的和差,得∠AOC=∠BOC+∠AOB=90°+60°=150°.
由ON平分∠AOC得,∠AON=
| 1 |
| 2 |
| 1 |
| 2 |
由角的和差,得
∠BON=∠AON-∠AOB=75°-60°=15°.
点评:本题考查了余角与补角,利用了补角的性质,角的和差,角平分线的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
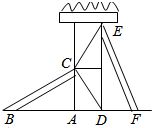 如图,有两个长度相等的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向上的长度DF相等,若∠ABC=32°,则∠DFE的度数为( )
如图,有两个长度相等的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向上的长度DF相等,若∠ABC=32°,则∠DFE的度数为( )| A、32° | B、28° |
| C、58° | D、45° |
关于x的方程2ax2-(8a+1)x+8a=0有实数根,则整数a的最小值是( )
| A、-2 | B、-1 | C、0 | D、1 |
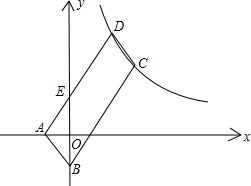 如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-2),顶点C、D在双曲线y=
如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-2),顶点C、D在双曲线y=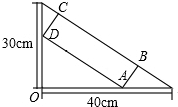 在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上.
在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上. 如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G,求证:AC•DG=AG•DF.
如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G,求证:AC•DG=AG•DF. 如图所示为六月份某水库的水位图.由于从5号连续降雨,7号到达警戒水位20m,于是从7号开始开闸泻洪,并加固加高堤坝,10号到达30m的危险水位时停止了下雨,水位开始回落.请回答下列问题:
如图所示为六月份某水库的水位图.由于从5号连续降雨,7号到达警戒水位20m,于是从7号开始开闸泻洪,并加固加高堤坝,10号到达30m的危险水位时停止了下雨,水位开始回落.请回答下列问题: