题目内容
已知a、b、c满足|a-2
|+
+(c-3
)2=0
(1)求a、b、c的值.
(2)试问:以a、b、c为三边长能否构成三角形,请求出这个三角形的周长,如不能构成三角形,请说明理由.
| 2 |
| b-5 |
| 2 |
(1)求a、b、c的值.
(2)试问:以a、b、c为三边长能否构成三角形,请求出这个三角形的周长,如不能构成三角形,请说明理由.
考点:二次根式的应用,三角形三边关系
专题:
分析:(1)根据非负数的性质来求a、b、c的值;
(2)三角形的三边关系:三角形两边之和大于第三边.
(2)三角形的三边关系:三角形两边之和大于第三边.
解答:解:(1)∵|a-2
|+
+(c-3
)2=0,
∴a-2
=0,
=0,c-3
=0,
解得 a=2
,b=5,c=3
;
(2)以a、b、c为三边长不能构成三角形.理由如下:
由(1)知,a=2
,b=5,c=3
.
∵5<2
+3
=5
,即b<a+c,
∴以a、b、c为三边长不能构成三角形.
| 2 |
| b-5 |
| 2 |
∴a-2
| 2 |
| b-5 |
| 2 |
解得 a=2
| 2 |
| 2 |
(2)以a、b、c为三边长不能构成三角形.理由如下:
由(1)知,a=2
| 2 |
| 2 |
∵5<2
| 2 |
| 2 |
| 2 |
∴以a、b、c为三边长不能构成三角形.
点评:本题考查的是非负数的性质及三角形的三边关系,熟知任意一个数的绝对值或偶次方都是非负数是解答此题的关键.

练习册系列答案
相关题目
 如图,点A、B、C是直线l上的三个点,图中共有射线条数为( )
如图,点A、B、C是直线l上的三个点,图中共有射线条数为( )| A、2条 | B、3条 | C、4条 | D、6条 |
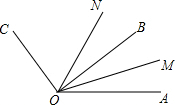 如图,已知∠AOB在∠AOC内部,∠BOC=90°,OM、ON分别是∠AOB,∠AOC的平分线,∠AOB与∠COM互补,求∠BON的度数.
如图,已知∠AOB在∠AOC内部,∠BOC=90°,OM、ON分别是∠AOB,∠AOC的平分线,∠AOB与∠COM互补,求∠BON的度数.
 如图,在Rt△ABC中,∠ACB=90°,BC=2cm,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,且∠F=∠A,若AE=3cm,则CF=
如图,在Rt△ABC中,∠ACB=90°,BC=2cm,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,且∠F=∠A,若AE=3cm,则CF=