题目内容
已知PA,PB切⊙O于点A,B,若⊙O的半径为
cm,∠APB=60°,则点P到圆心的距离为 cm.
| 3 |
考点:切线的性质
专题:计算题
分析:连结OA、OB,如图,根据切线长定理得到OP平分∠APB,则∠APO=
∠APB=30°,再根据切线的性质得∠OAP=90°,然后在Rt△OAP中利用含30度的直角三角形三边的关系求出OP即可.
| 1 |
| 2 |
解答:解: 连结OA、OB,如图,
连结OA、OB,如图,
∵PA、PB切⊙O于点A,B,
∴OP平分∠APB,
∴∠APO=
∠APB=30°,
∵PA为⊙的切线,
∴OA⊥PA,
∴∠OAP=90°,
在Rt△OAP中,∵∠APO=30°,OA=
cm,
∴OP=2OA=2
cm.
即点P到圆心的距离为2
cm.
故答案为2
.
 连结OA、OB,如图,
连结OA、OB,如图,∵PA、PB切⊙O于点A,B,
∴OP平分∠APB,
∴∠APO=
| 1 |
| 2 |
∵PA为⊙的切线,
∴OA⊥PA,
∴∠OAP=90°,
在Rt△OAP中,∵∠APO=30°,OA=
| 3 |
∴OP=2OA=2
| 3 |
即点P到圆心的距离为2
| 3 |
故答案为2
| 3 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了切线长定理和含30度的直角三角形三边的关系.

练习册系列答案
相关题目
如果两圆的半径分别为4和6,圆心距为12,那么这两圆的位置关系是( )
| A、外切 | B、内含 | C、相交 | D、外离 |
 如图,CD是Rt△ABC斜边AB上的高,E为BC的中点,ED的延长线交CA于F.求证:AC•CF=BC•DF.
如图,CD是Rt△ABC斜边AB上的高,E为BC的中点,ED的延长线交CA于F.求证:AC•CF=BC•DF.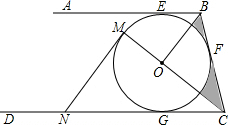 如图,AB、BC、CD分别于⊙O相切于E、F、G,且AB∥CD,连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.
如图,AB、BC、CD分别于⊙O相切于E、F、G,且AB∥CD,连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.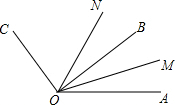 如图,已知∠AOB在∠AOC内部,∠BOC=90°,OM、ON分别是∠AOB,∠AOC的平分线,∠AOB与∠COM互补,求∠BON的度数.
如图,已知∠AOB在∠AOC内部,∠BOC=90°,OM、ON分别是∠AOB,∠AOC的平分线,∠AOB与∠COM互补,求∠BON的度数. 如图,在梯形ABCD中,AD∥BC,E和F分别是BD,AC的中点,若BC=10,AD=6,则线段EF的长为( )
如图,在梯形ABCD中,AD∥BC,E和F分别是BD,AC的中点,若BC=10,AD=6,则线段EF的长为( )