题目内容
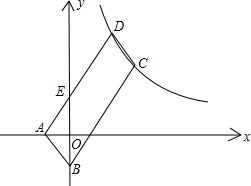 如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-2),顶点C、D在双曲线y=
如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-2),顶点C、D在双曲线y=| k |
| x |
(1)△AEB与△DEB的面积比为
(2)若点D的坐标为(m,n),则点C的坐标为
(3)求反比例函数的解析式.
考点:反比例函数综合题
专题:
分析:(1)如图,连接BD,根据平行四边形的性质得到:S△ABD=S△CBD,然后结合已知条件“四边形BCDE的面积是△ABE面积的5倍”填空;
(2)分别过C、D作x轴的垂线,垂足为F、G,过C点作CH⊥DG,垂足为H,根据CD∥AB,CD=AB可证△CDH≌△ABO,则CH=AO=1,DH=OB=2,由此根据点D的坐标求得点C的坐标;
(3)C、D两点在双曲线y=
上,则(m+1)(n-2)=mn,解得m、n的数量关系,设直线AD解析式为y=ax+b(a≠0),将A、D两点坐标代入求解析式,确定E点坐标,求S△ABE,根据S四边形BCDE=5S△ABE,列方程求m、n的值,根据k=mn求解.
(2)分别过C、D作x轴的垂线,垂足为F、G,过C点作CH⊥DG,垂足为H,根据CD∥AB,CD=AB可证△CDH≌△ABO,则CH=AO=1,DH=OB=2,由此根据点D的坐标求得点C的坐标;
(3)C、D两点在双曲线y=
| k |
| x |
解答: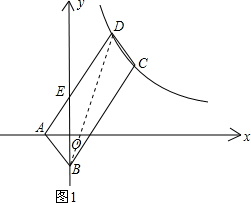 解:(1)如图,连接BD.
解:(1)如图,连接BD.
∵四边形ABCD是平行四边形,
∴S△ABD=S△CBD.
∵四边形BCDE的面积是△ABE面积的5倍,
∴S△ABE=
S平行四边形ABCD=
S△ABD,
∴S△DEB=
S△ABD,
∴S△ABE:S△DEB=1:2;
故答案是:1:2;
(2)如图2,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,
∵ABCD是平行四边形,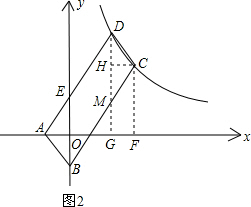
∴∠ABC=∠ADC,
∵BO∥DG,
∴∠OBC=∠GDE,
∴∠HDC=∠ABO,
在△CDH与△ABO中,
,
∴△CDH≌△ABO(AAS),
∴CH=AO=1,DH=OB=2.
∴点D的坐标为(m,n),则点C的坐标为(m+1,n-2).
故答案是:(m+1,n-2).
(3)由(2)知,设C(m+1,n-2),D(m,n),
则(m+1)(n-2)=mn=k,
解得n=2m+2,则D的坐标是(m,2m+2),
设直线AD解析式为y=ax+b(a≠0),将A、D两点坐标代入得
,
由①得:a=b,代入②得:mb+b=2m+2,
即b(m+1)=2(m+1),解得b=2,
则
,
∴y=2x+2,E(0,2),BE=4,
∴S△ABE=
×BE×AO=2,
∵S四边形BCDE=5S△ABE=5×
×4×1=10,
∵S四边形BCDE=S△ABE+S四边形BEDM=10,
即2+4×m=10,
解得m=2,
∴n=2m+2=6,
∴k=mn=2×6=12.
则该反比例函数的解析式为:y=
.
 解:(1)如图,连接BD.
解:(1)如图,连接BD.∵四边形ABCD是平行四边形,
∴S△ABD=S△CBD.
∵四边形BCDE的面积是△ABE面积的5倍,
∴S△ABE=
| 1 |
| 6 |
| 1 |
| 3 |
∴S△DEB=
| 2 |
| 3 |
∴S△ABE:S△DEB=1:2;
故答案是:1:2;
(2)如图2,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,
∵ABCD是平行四边形,

∴∠ABC=∠ADC,
∵BO∥DG,
∴∠OBC=∠GDE,
∴∠HDC=∠ABO,
在△CDH与△ABO中,
|
∴△CDH≌△ABO(AAS),
∴CH=AO=1,DH=OB=2.
∴点D的坐标为(m,n),则点C的坐标为(m+1,n-2).
故答案是:(m+1,n-2).
(3)由(2)知,设C(m+1,n-2),D(m,n),
则(m+1)(n-2)=mn=k,
解得n=2m+2,则D的坐标是(m,2m+2),
设直线AD解析式为y=ax+b(a≠0),将A、D两点坐标代入得
|
由①得:a=b,代入②得:mb+b=2m+2,
即b(m+1)=2(m+1),解得b=2,
则
|
∴y=2x+2,E(0,2),BE=4,
∴S△ABE=
| 1 |
| 2 |
∵S四边形BCDE=5S△ABE=5×
| 1 |
| 2 |
∵S四边形BCDE=S△ABE+S四边形BEDM=10,
即2+4×m=10,
解得m=2,
∴n=2m+2=6,
∴k=mn=2×6=12.
则该反比例函数的解析式为:y=
| 12 |
| x |
点评:本题考查了反比例函数的综合运用.关键是通过作辅助线,将图形分割,寻找全等三角形,利用边的关系设双曲线上点的坐标,根据面积关系,列方程求解.

练习册系列答案
相关题目
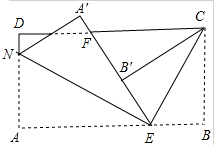 如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,求∠NEM的度数.
如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,求∠NEM的度数. 如图,点A、B、C是直线l上的三个点,图中共有射线条数为( )
如图,点A、B、C是直线l上的三个点,图中共有射线条数为( )| A、2条 | B、3条 | C、4条 | D、6条 |
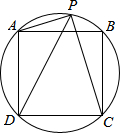 正方形ABCD的四点在☉O上,若P是弧AB上一点,请确定PA+PC与PD之间的数量关系,并证明你的结论.
正方形ABCD的四点在☉O上,若P是弧AB上一点,请确定PA+PC与PD之间的数量关系,并证明你的结论.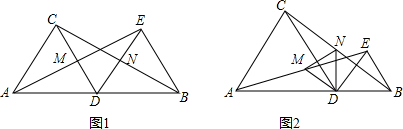
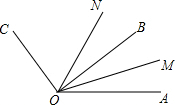 如图,已知∠AOB在∠AOC内部,∠BOC=90°,OM、ON分别是∠AOB,∠AOC的平分线,∠AOB与∠COM互补,求∠BON的度数.
如图,已知∠AOB在∠AOC内部,∠BOC=90°,OM、ON分别是∠AOB,∠AOC的平分线,∠AOB与∠COM互补,求∠BON的度数.