题目内容
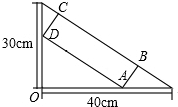 在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上.
在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上.(1)设矩形的一边BC为x,那么AB边的长度如何表示?
(2)设矩形的面积为y平方米,当x取何值时,y的最大值为多少?
考点:相似三角形的判定与性质,二次函数的最值
专题:
分析:(1)易求sin∠AEB、cos∠OAD的值,设BC=x,即可求得OA的值,即可求得AE的长,即可求得AB的值,即可解题;
(2)根据矩形的面积=AB•BC即可求得y关于x的二次函数值,即可求得y的最大值,即可解题.
(2)根据矩形的面积=AB•BC即可求得y关于x的二次函数值,即可求得y的最大值,即可解题.
解答:解:(1)

∵AD∥BC,
∴tan∠OAD=tan∠AEB=
=
,
∴sin∠AEB=
,cos∠OAD=
,
设BC=x,则AD=x,
∴OA=AD•cos∠OAD=
x,
∴AE=40-
x,
∴AB=AE•sin∠AEB=
(40-
x)=24-
x;
(2)设矩形的面积为y平方米,
则y=AB•BC=(24-
x)x=-
x2+24x,
当x=-
=-
=25时,y有最大值为300cm2.

∵AD∥BC,
∴tan∠OAD=tan∠AEB=
| 30 |
| 40 |
| 3 |
| 4 |
∴sin∠AEB=
| 3 |
| 5 |
| 4 |
| 5 |
设BC=x,则AD=x,
∴OA=AD•cos∠OAD=
| 4 |
| 5 |
∴AE=40-
| 4 |
| 5 |
∴AB=AE•sin∠AEB=
| 3 |
| 5 |
| 4 |
| 5 |
| 12 |
| 25 |
(2)设矩形的面积为y平方米,
则y=AB•BC=(24-
| 12 |
| 25 |
| 12 |
| 25 |
当x=-
| b |
| 2a |
| 24 | ||
2×(-
|
点评:本题考查了直角三角形中三角函数值的运用,考查了直角三角形中三角函数的求值,考查了二次函数的最值问题,本题中求二次函数的最大值是解题的关键.

练习册系列答案
相关题目
 如图,点A、B、C是直线l上的三个点,图中共有射线条数为( )
如图,点A、B、C是直线l上的三个点,图中共有射线条数为( )| A、2条 | B、3条 | C、4条 | D、6条 |
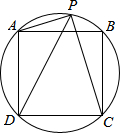 正方形ABCD的四点在☉O上,若P是弧AB上一点,请确定PA+PC与PD之间的数量关系,并证明你的结论.
正方形ABCD的四点在☉O上,若P是弧AB上一点,请确定PA+PC与PD之间的数量关系,并证明你的结论. 如图,CD是Rt△ABC斜边AB上的高,E为BC的中点,ED的延长线交CA于F.求证:AC•CF=BC•DF.
如图,CD是Rt△ABC斜边AB上的高,E为BC的中点,ED的延长线交CA于F.求证:AC•CF=BC•DF. 如图,等边△ABC的边长为10,BD⊥AC于点D,点M在AB上,AM=4,在BD上找一点P,使PN+PA最小,求这个最小值.
如图,等边△ABC的边长为10,BD⊥AC于点D,点M在AB上,AM=4,在BD上找一点P,使PN+PA最小,求这个最小值.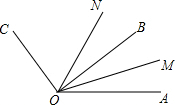 如图,已知∠AOB在∠AOC内部,∠BOC=90°,OM、ON分别是∠AOB,∠AOC的平分线,∠AOB与∠COM互补,求∠BON的度数.
如图,已知∠AOB在∠AOC内部,∠BOC=90°,OM、ON分别是∠AOB,∠AOC的平分线,∠AOB与∠COM互补,求∠BON的度数.