题目内容
1.【折纸活动】矩形纸片的宽度MN为6cm第一步,在矩形纸片的一端,利用图1的方法折出一个正方形,然后把纸片展平.
第二步,如图2,把这个正方形折成两个全等的矩形,再把纸片展平.第三步,折出内侧矩形的对角线AB,并把它折到图3中所示的AD处.
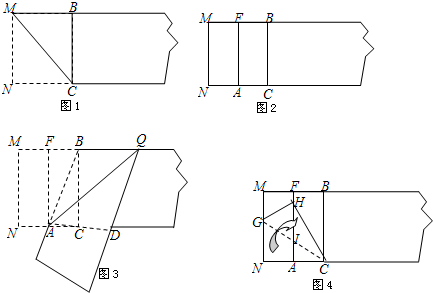
【问题解决】
(1)在图3中,证明四边形ABQD是菱形;
(2)在图3中,求四边形ABQD的面积;
(3)在图2中,将正方形的边CN沿CG折,使点N落在AF上的点H处,如图4所示,求四边形MGHF的周长.
分析 (1)利用翻折变换的性质以及平行四边形的判定得出即可;
(2)根据正方形的性质得到AF,BF的长度,根据勾股定理得到AB的长度,然后根据菱形的面积公式即可得到结论;
(3)由平行线等分线段定理,得出GI=CI,然后解直角三角形得到AH的长度,于是得到FH的长度,即可得到结论.
解答 解:(1)由翻折知,AB=AD,∠BAQ=∠DAQ,
∵BQ∥AD
∴∠BQA=∠DAQ.
∴∠BQA=∠BAQ.
∴BA=BQ.
∴AD=BQ.
∴四边形ADQB是平行四边形.
∴平行四边形ADQB是菱形;
(2)由题意得:AF=MN=BM=BC=6cm,BF=$\frac{1}{2}$BM=3cm,
∴AB=$\sqrt{A{F}^{2}+B{F}^{2}}$=3$\sqrt{5}$cm,
∴S四边形ADQB=3$\sqrt{5}$×6=18$\sqrt{5}$cm2;
(3)如图,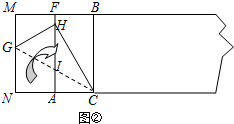
设CG交AF于点I,由平行线等分线段定理,
∵MN∥AF∥BC,且NA=CA,
∴GI=CI.
∴在Rt△GHC中,GI=CI=HI.
∴∠IHC=∠ICH.
又∠ICA=∠ICH.∠IHC=∠BCH.
∴∠ICA=∠ICH=∠BCH=∠AHC=30°,
∴AH=$\frac{\sqrt{3}}{2}$CH=3$\sqrt{3}$,
∴FH=6-3$\sqrt{3}$,
∴四边形MGHF的周长=MG+GH+FH+MF=MN+FM+FH=6+3+6-3$\sqrt{3}$=15-3$\sqrt{3}$.
点评 此题主要考查了几何变换以及翻折变换的性质以及正方形的性质和勾股定理等知识,熟练利用勾股定理以及翻折变换的性质是解题关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
9.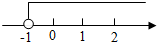 已知关于x的不等式2x-a>-3的解集在数轴上表示如图所示,则a的值等于( )
已知关于x的不等式2x-a>-3的解集在数轴上表示如图所示,则a的值等于( )
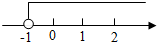 已知关于x的不等式2x-a>-3的解集在数轴上表示如图所示,则a的值等于( )
已知关于x的不等式2x-a>-3的解集在数轴上表示如图所示,则a的值等于( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
13.在数轴上到原点的距离等于5的点表示的数是( )
| A. | 5 | B. | 2 | C. | 5或-2 | D. | 5或-5 |
11. 张萌将直尺ABCD(AD∥BC)和三角板EFG按如图所示的方式摆放,点F在BC上,若∠BFE=20°,∠EFG=90°,则∠DMF的度数为( )
张萌将直尺ABCD(AD∥BC)和三角板EFG按如图所示的方式摆放,点F在BC上,若∠BFE=20°,∠EFG=90°,则∠DMF的度数为( )
 张萌将直尺ABCD(AD∥BC)和三角板EFG按如图所示的方式摆放,点F在BC上,若∠BFE=20°,∠EFG=90°,则∠DMF的度数为( )
张萌将直尺ABCD(AD∥BC)和三角板EFG按如图所示的方式摆放,点F在BC上,若∠BFE=20°,∠EFG=90°,则∠DMF的度数为( )| A. | 80° | B. | 70° | C. | 60° | D. | 50° |