题目内容
 如图,已知∠1=∠2,∠3=∠4,∠5=∠A,求证:BE∥CF.
如图,已知∠1=∠2,∠3=∠4,∠5=∠A,求证:BE∥CF.考点:平行线的判定与性质
专题:证明题
分析:可先证明BC∥AF,可得到∠A+∠ABC=180°,结合条件可得∠2+∠3+∠5=180°,可得到∠1+∠3+∠5=180°,可证明BE∥CF.
解答:证明:
∵∠3=∠4,
∴AF∥BC,
∴∠A+∠ABC=180°,
即∠A+∠2+∠3=180°,
又∠A=∠5,∠1=∠2,
∴∠1+∠5+∠3=180°,
∴∠EBC+∠FCB=180°,
∴BE∥CF.
∵∠3=∠4,
∴AF∥BC,
∴∠A+∠ABC=180°,
即∠A+∠2+∠3=180°,
又∠A=∠5,∠1=∠2,
∴∠1+∠5+∠3=180°,
∴∠EBC+∠FCB=180°,
∴BE∥CF.
点评:本题主要考查平行线的性质和判定,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 小明到工厂去进行社会实践活动,发现工人师傅生产了一种如图所示的零件,要求AB∥CD,∠BAE=30°.∠AED=70°.小明发现工人师傅只是量出∠BAE=30°.∠AED=70°后,又量了∠EDC=40°,就说AB与CD肯定是平行的,你知道是什么原因吗?
小明到工厂去进行社会实践活动,发现工人师傅生产了一种如图所示的零件,要求AB∥CD,∠BAE=30°.∠AED=70°.小明发现工人师傅只是量出∠BAE=30°.∠AED=70°后,又量了∠EDC=40°,就说AB与CD肯定是平行的,你知道是什么原因吗? 如图,
如图, 如图,延长△ABC的中线BD至E,使∠DAE=∠BCA.四边形ABCE是平行四边形吗?你找到了几种证法?
如图,延长△ABC的中线BD至E,使∠DAE=∠BCA.四边形ABCE是平行四边形吗?你找到了几种证法? 如图,BD平分∠ABC,∠ABD=50°,∠FEC=100°,证明:AB∥EF.
如图,BD平分∠ABC,∠ABD=50°,∠FEC=100°,证明:AB∥EF. 如图,直线y=ax+b(a≠0)与y=cx+d(c≠0)相交于点P,则关于x,y的方程组
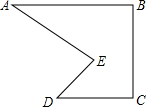
如图,直线y=ax+b(a≠0)与y=cx+d(c≠0)相交于点P,则关于x,y的方程组 如图,某公路上A,B两点的正南方有D,C两村庄,现要在公路AB上建一个车站E,使C,D两村到E站的距离相等,已知AB=50km,DA=20km,CB=10km,请你设计出E站的位置,并计算车站E距A点多远?
如图,某公路上A,B两点的正南方有D,C两村庄,现要在公路AB上建一个车站E,使C,D两村到E站的距离相等,已知AB=50km,DA=20km,CB=10km,请你设计出E站的位置,并计算车站E距A点多远?