题目内容
△ABC中，DE是其中位线，点O是DE上的一个动点，AO延长线交BC于F，当O运动到DE的什么位置时，四边形ADFE为平行四边形？
考点：平行四边形的判定
专题：
分析：利用三角形中位线的性质得出DE∥BC，BD=AD，AE=EC，进而利用对角线互相平分的四边形是平行四边形，进而得出答案．
解答：
解：如图所示：当O在DE的中点时，四边形ADFE为平行四边形．
理由：∵△ABC中，DE是其中位线，
∴DE∥BC，BD=AD，AE=EC，
∴AO=CO，
∵DO=EO，
∴四边形ADFE为平行四边形．
解：如图所示：当O在DE的中点时，四边形ADFE为平行四边形．理由：∵△ABC中，DE是其中位线，
∴DE∥BC，BD=AD，AE=EC，
∴AO=CO，
∵DO=EO，
∴四边形ADFE为平行四边形．
点评：此题主要考查了平行四边形的判定以及三角形的中位线，正确利用平行线分线段成比例定理得出AO=FO是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知∠1=∠2，∠3=∠4，∠5=∠A，求证：BE∥CF．
如图，在四边形ABCD中，∠A与∠C互补，∠ABC、∠ADC的平分线分别于CD、AB相交于点E、F．∠1与∠2有怎样的数量关系？为什么？
如图，已知∠1=∠2，∠3=∠4，AD∥BC，试证明∠5=∠6．
如图，在Rt△ABC中，∠ACB=90°，且AB=
已知，如图，MN∥PQ，∠MAC，∠PCA的平分线AB，CB相交于点B，∠NAC，∠ACQ的平分线AD，CD相交于点D，四边形ABCD是矩形吗？为什么？下列根式中，最简二次根式是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
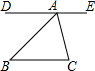如图，直线DE经过点A，DE∥BC，∠B=44°，∠C=85°．