题目内容
6.某特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低1元,则平均每天的销售可增加10千克.(1)若该商品销售这种核桃要想平均每天获利2240元
①每千克核桃应降低多少元?
②在平均每天获利不变的情况下,为尽可能吸引顾客,赢得市场,该店应按原售价的几折出售?
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少元时,才能使平均每天获得的利润最大?
分析 (1)①设每千克水果应降价x元,利用销售量×每件利润=2240元列出方程求解即可;
②为了让利于顾客因此应下降6元,求出此时的销售单价即可确定几折;
(2)设每天获得的利润为W,销售价格为x,列出W与x的函数关系式即可解答.
解答 解:(1)①设每千克水果应降价x元,
根据题意,得:(60-x-40)(100+10x)=2240,
解得:x1=4,x2=6,
答:每千克水果应降价4元或6元;
②由①可知每千克水果可降价4元或6元.
因为要尽可能让利于顾客,所以每千克水果应降价6元.
此时,售价为:60-6=54(元),$\frac{54}{60}$×100%=90%.
答:该店应按原售价的九折出售.
(2)设每天获得的利润为W,销售价格为x,则
W=(x-40)[100+10(60-x)]
=(x-40)(-10x+700)
=-10x2+1100x-28000
=-10(x-55)2+2250.
∴若不考虑其他因素,销售价格定为55时,才能使平均每天获得的利润最大.
点评 本题考查了一元二次方程的应用以及二次函数的应用,解题的关键是根据题目中的等量关系列出方程和函数关系式.

练习册系列答案
相关题目
16.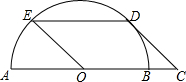 如图,点C是半圆O的直径AB的延长线上一点.CD与半圆O相切,D为切点,过点D作DE∥AB交半圆O于点E.若四边形OCDE是平行四边形,CD=4,则ED的长为( )
如图,点C是半圆O的直径AB的延长线上一点.CD与半圆O相切,D为切点,过点D作DE∥AB交半圆O于点E.若四边形OCDE是平行四边形,CD=4,则ED的长为( )
 如图,点C是半圆O的直径AB的延长线上一点.CD与半圆O相切,D为切点,过点D作DE∥AB交半圆O于点E.若四边形OCDE是平行四边形,CD=4,则ED的长为( )
如图,点C是半圆O的直径AB的延长线上一点.CD与半圆O相切,D为切点,过点D作DE∥AB交半圆O于点E.若四边形OCDE是平行四边形,CD=4,则ED的长为( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{6}$ | D. | 3$\sqrt{3}$ |
18. 如图所示的物体是一个实心几何体,其俯视图是( )
如图所示的物体是一个实心几何体,其俯视图是( )
 如图所示的物体是一个实心几何体,其俯视图是( )
如图所示的物体是一个实心几何体,其俯视图是( )| A. |  | B. |  | C. |  | D. |  |
15.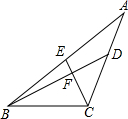 已知△ABC中,D,E分别是AC,AB边上的中点,BD⊥CE于点F,CE=2,BD=4,则△ABC的面积为( )
已知△ABC中,D,E分别是AC,AB边上的中点,BD⊥CE于点F,CE=2,BD=4,则△ABC的面积为( )
 已知△ABC中,D,E分别是AC,AB边上的中点,BD⊥CE于点F,CE=2,BD=4,则△ABC的面积为( )
已知△ABC中,D,E分别是AC,AB边上的中点,BD⊥CE于点F,CE=2,BD=4,则△ABC的面积为( )| A. | $\frac{16}{3}$ | B. | 8 | C. | 4 | D. | 6 |
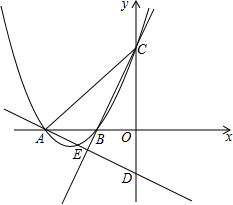 如图,抛物线y=ax2+bx+6与x轴分别相交于点A、B,与y轴相交于点C,过点A的直线y=-$\frac{1}{2}$x+m与y轴相交于点D,连接CB并延长,与直线AD相交于点E,若点A的坐标为(-8,0),E为AD的中点,
如图,抛物线y=ax2+bx+6与x轴分别相交于点A、B,与y轴相交于点C,过点A的直线y=-$\frac{1}{2}$x+m与y轴相交于点D,连接CB并延长,与直线AD相交于点E,若点A的坐标为(-8,0),E为AD的中点,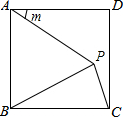 如图,在正方形ABCD中,边AD绕点A顺时针旋转角度m(0°<m<360°),得到线段AP,连接PB,PC.当△BPC是等腰三角形时,m的值为30°或60°或150°或300°.
如图,在正方形ABCD中,边AD绕点A顺时针旋转角度m(0°<m<360°),得到线段AP,连接PB,PC.当△BPC是等腰三角形时,m的值为30°或60°或150°或300°.