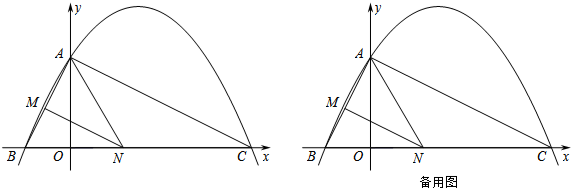题目内容
7. 如图,在Rt△ABC中,∠C=90°,直线DE是斜边AB的垂直平分线交AC于D.若AC=8,BC=6,则△DBC的周长为( )
如图,在Rt△ABC中,∠C=90°,直线DE是斜边AB的垂直平分线交AC于D.若AC=8,BC=6,则△DBC的周长为( )| A. | 12 | B. | 14 | C. | 16 | D. | 无法计算 |
分析 根据线段的垂直平分线上的点到线段的两个端点的距离相等得到DA=DB,根据三角形周长公式求出周长.
解答 解:∵DE是AB的垂直平分线,
∴DA=DB,
△DBC的周长为CB+CD+DB
=CB+CD+DA
=BC+CA
=6+8
=14,
故选:B.
点评 此题主要考查线段的垂直平分线的性质等几何知识,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
相关题目
2.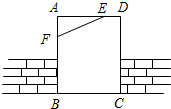 如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
 如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )| A. | 两点之间,线段最短 | B. | 直角三角形的两个锐角互余 | ||
| C. | 三角形三个内角和等于180° | D. | 三角形具有稳定性 |
16.为迎接“六一”儿童节,某儿童品牌玩具专卖店购进了A、B两类玩具,其中A类玩具的进价比B类玩具的进价每个多3元,经调查:用900元购进A类玩具的数量与用750元购进B类玩具的数量相同.设A类玩具的进价为m元/个,根据题意可列分式方程为( )
| A. | $\frac{900}{m}=\frac{750}{m+3}$ | B. | $\frac{900}{m+3}=\frac{750}{m}$ | C. | $\frac{900}{m}=\frac{750}{m-3}$ | D. | $\frac{900}{m-3}=\frac{750}{m}$ |
16.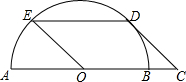 如图,点C是半圆O的直径AB的延长线上一点.CD与半圆O相切,D为切点,过点D作DE∥AB交半圆O于点E.若四边形OCDE是平行四边形,CD=4,则ED的长为( )
如图,点C是半圆O的直径AB的延长线上一点.CD与半圆O相切,D为切点,过点D作DE∥AB交半圆O于点E.若四边形OCDE是平行四边形,CD=4,则ED的长为( )
 如图,点C是半圆O的直径AB的延长线上一点.CD与半圆O相切,D为切点,过点D作DE∥AB交半圆O于点E.若四边形OCDE是平行四边形,CD=4,则ED的长为( )
如图,点C是半圆O的直径AB的延长线上一点.CD与半圆O相切,D为切点,过点D作DE∥AB交半圆O于点E.若四边形OCDE是平行四边形,CD=4,则ED的长为( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{6}$ | D. | 3$\sqrt{3}$ |
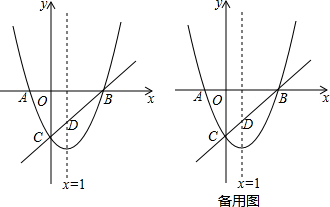
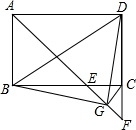 如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论: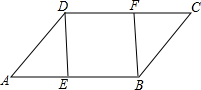 已知:如图,点E、F分别是?ABCD中AB、DC边上的点,且AE=CF,连接DE、EF.求证:四边形DEBF是平行四边形.
已知:如图,点E、F分别是?ABCD中AB、DC边上的点,且AE=CF,连接DE、EF.求证:四边形DEBF是平行四边形.