题目内容
1．求不等式组的正整数解$\left\{\begin{array}{l}{\frac{x-2}{7}≥0}\\{-2x-3＜3（\frac{1}{3}-x）}\end{array}\right.$．分析 先求出不等式组中每个不等式的解集，然后求出其公共解集，最后求其正整数解即可
解答 解：$\left\{\begin{array}{l}{\frac{x-2}{7}≥0①}\\{-2x-3＜3（\frac{1}{3}-x）②}\end{array}\right.$
解不等式①得：x≥2，
解不等式②得：x＜4，
∴不等式组的解集为2≤x＜4，
∴不等式组的正整数解为2、3．
点评 本题考查了解一元一次不等式组，不等式组的整数解的应用，求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．
练习册系列答案
相关题目
12．
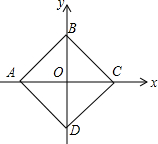以正方形ABCD的对角线AC、BD所在直线为坐标轴，建立平面直角坐标系，如图所示，已知点A的坐标是（-$\sqrt{2}$，0），现将正方形ABCD绕原点O顺时针旋转45°，则旋转后点C的对应点坐标是（ ）
以正方形ABCD的对角线AC、BD所在直线为坐标轴，建立平面直角坐标系，如图所示，已知点A的坐标是（-$\sqrt{2}$，0），现将正方形ABCD绕原点O顺时针旋转45°，则旋转后点C的对应点坐标是（ ）| A． | （$\sqrt{2}$，$\sqrt{2}$） | B． | （$\sqrt{2}$，-$\sqrt{2}$） | C． | （-1，1） | D． | （1，-1） |
9．反比例函数$y=\frac{2}{x}$的图象上有三个点（x1，y1），（x2，y2），（x3，y3），其中x1＜x2＜0＜x3，则y1、y2、y3的大小关系是（ ）
| A． | y1＜y2＜y3 | B． | y2＜y1＜y3 | C． | y3＜y1＜y2 | D． | y3＜y2＜y1 |
16．
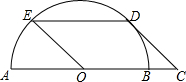如图，点C是半圆O的直径AB的延长线上一点．CD与半圆O相切，D为切点，过点D作DE∥AB交半圆O于点E．若四边形OCDE是平行四边形，CD=4，则ED的长为（ ）
如图，点C是半圆O的直径AB的延长线上一点．CD与半圆O相切，D为切点，过点D作DE∥AB交半圆O于点E．若四边形OCDE是平行四边形，CD=4，则ED的长为（ ）| A． | 4 | B． | 4$\sqrt{2}$ | C． | 2$\sqrt{6}$ | D． | 3$\sqrt{3}$ |
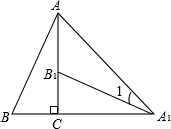如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A1B1C，连结AA1，若∠AA1B1=15°，则∠B的度数是60°．
10．下列函数中，y是x的正比例函数的是（ ）
| A． | y=2x-1 | B． | y=$\frac{3}{x}$ | C． | y=2x | D． | y=$\frac{2}{x}$ |