题目内容
12.平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,-1),点C在y轴上,如果三角形ABC的面积等于6,则点C的坐标为(0,5)或(0,-7).分析 设点C坐标为(0,y),可得BC=|y+1|,OA=2,由ABC的面积等于6列方程求出y即可得.
解答 解:设点C坐标为(0,y),
∵点B的坐标为(0,-1),点A的坐标为(2,0),
则BC=|y+1|,OA=2,
∵S△ABC=$\frac{1}{2}$BC•OA,
∴$\frac{1}{2}$|y+1|•2=6,
则|y+1|=6,即y+1=6或y+1=-6,
解得:y=5或y=-7,
∴点C的坐标为(0,5)或(0,-7),
故答案为:(0,5)或(0,-7).
点评 本题考查了三角形的面积,坐标与图形性质,要注意B、C两点间的距离的表示是解题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
3.下列运算中,正确的是( )
| A. | a3•a2=a6 | B. | b4+b4=b8 | C. | a8÷a2=a4 | D. | (-3p2q)3=-27p6q3 |
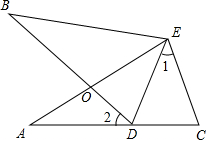 如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.