题目内容
1.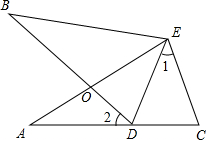 如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
分析 (1)根据全等三角形的判定即可判断△AEC≌△BED;
(2)由(1)可知:EC=ED,∠C=∠BDE,根据等腰三角形的性质即可知∠C的度数,从而可求出∠BDE的度数;
解答 解:(1)证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
$\left\{\begin{array}{l}∠A=∠B\\ AE=BE\\∠AEC=∠BED\end{array}\right.$,
∴△AEC≌△BED(ASA).
(2)∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=42°,
∴∠C=∠EDC=69°,
∴∠BDE=∠C=69°.
点评 本题考查全等三角形,解题的关键是熟练运用全等三角形的性质与判定,本题属于中等题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知点(-1,y1),(4,y2)在一次函数y=3x-2的图象上,则y1,y2,0的大小关系是( )
| A. | 0<y1<y2 | B. | y1<0<y2 | C. | y1<y2<0 | D. | y2<0<y1 |
6.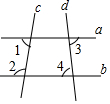 如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4度数是( )
如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4度数是( )
 如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4度数是( )
如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4度数是( )| A. | 80° | B. | 85° | C. | 95° | D. | 100° |
11.某商场将一种商品A按标价九折出售,仍获利10%,若商品A标价为33元,那么商品进价为( )
| A. | 31元 | B. | 30.2元 | C. | 29.7元 | D. | 27元 |
 如图是我市某连续7天的最高气温与最低气温的变化图,根据图中信息可知,这7天中最大的日温差是11℃.
如图是我市某连续7天的最高气温与最低气温的变化图,根据图中信息可知,这7天中最大的日温差是11℃.
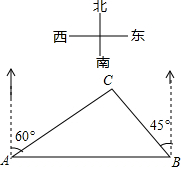 如图,在一笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头 A北偏东60°的方向,在码头 B北偏西45°的方向,AC=4km.游客小张准备从观光岛屿C乘船沿CA回到码头A或沿CB回到码头B,设开往码头A、B的游船速度分别为v1、v2,若回到 A、B所用时间相等,则$\frac{v_1}{v_2}$=$\sqrt{2}$(结果保留根号).
如图,在一笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头 A北偏东60°的方向,在码头 B北偏西45°的方向,AC=4km.游客小张准备从观光岛屿C乘船沿CA回到码头A或沿CB回到码头B,设开往码头A、B的游船速度分别为v1、v2,若回到 A、B所用时间相等,则$\frac{v_1}{v_2}$=$\sqrt{2}$(结果保留根号).