题目内容
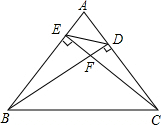 如图,BD、CE是△ABC的高.
如图,BD、CE是△ABC的高.(1)与△AEC相似的三角形有哪些?(用相似符号表示)
(2)△ADE与△ABC相似吗?为什么?
(3)若∠A=60°,求△ADE与△ABC的面积比.
考点:相似三角形的判定与性质
专题:
分析:(1)易证△AEC∽△ADB,△EFB∽△ADB,即可求得△AEC∽△DCF∽△EFB△ADB;
(2)易证
=
,根据∠A=∠A,即可证明△ADE∽△ABC;
(3)易证AB=2AD,AC=2AE,即可求得
的值,即可解题.
(2)易证
| AE |
| AD |
| AC |
| AB |
(3)易证AB=2AD,AC=2AE,即可求得
| S△ADE |
| S△ABC |
解答:解:(1)∵∠A=∠A,∠ADB=∠AEC,
∴△AEC∽△ADB,
∵∠ABD=∠EAF,∠ADB=∠AEC=90°,
∴△EFB∽△ADB,
∵∠ACE=∠DCF,∠AEC=∠FDC=90°,
∴△AEC∽△DCF,
∴△AEC∽△DCF∽△EFB△ADB;
(2)∵△AEC∽△ADB,
∴
=
,
∵∠A=∠A,
∴△ADE∽△ABC;
(3)∵∠A=60°,
∴AB=2AD,AC=2AE,
∴
=
=
.
∴△AEC∽△ADB,
∵∠ABD=∠EAF,∠ADB=∠AEC=90°,
∴△EFB∽△ADB,
∵∠ACE=∠DCF,∠AEC=∠FDC=90°,
∴△AEC∽△DCF,
∴△AEC∽△DCF∽△EFB△ADB;
(2)∵△AEC∽△ADB,
∴
| AE |
| AD |
| AC |
| AB |
∵∠A=∠A,
∴△ADE∽△ABC;
(3)∵∠A=60°,
∴AB=2AD,AC=2AE,
∴
| S△ADE |
| S△ABC |
| ||
|
| 1 |
| 4 |
点评:本题考查了相似三角形的判定,考查了相似三角形面积比等于相似比平方的性质,本题中求证△ADE∽△ABC是解题的关键.

练习册系列答案
相关题目
 如图,△ABC中,M为AC边的中点,E为AB上一点,且AE=
如图,△ABC中,M为AC边的中点,E为AB上一点,且AE= 如图,已知∠A=∠C,∠1与∠2互补,若∠1=∠C,请直接写出所有与∠A相等的角.
如图,已知∠A=∠C,∠1与∠2互补,若∠1=∠C,请直接写出所有与∠A相等的角.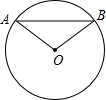 如图,已知⊙O的半径为30mm,弦AB=36mm,求点O到AB的距离及∠OAB的余弦值.
如图,已知⊙O的半径为30mm,弦AB=36mm,求点O到AB的距离及∠OAB的余弦值. 如图,点P是反比例函数的图象上一点,PA⊥x轴,S△PAO=6,则这个函数的解析式为
如图,点P是反比例函数的图象上一点,PA⊥x轴,S△PAO=6,则这个函数的解析式为