题目内容
16.在目前的八年级数学下册第二章《一元二次方程》中新增了一节选学内容,其中有这样的知识点:如果方程ax2+bx+c=0(a≠0)的两根是x1、x2,那么x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$,则若关于x的方程x2-(k-1)x+k+1=0的两个实数根满足关系式|x1-x2|=$\sqrt{13}$,则k的值为8或-2.分析 由|x1-x2|=$\sqrt{({x}_{1+}{x}_{2})^{2}-4{x}_{1}{x}_{2}}$和根与系数的关系即可求出k的值.
解答 解:
∵关于x的方程x2-(k-1)x+k+1=0的两个实数根x1、x2,
∴x1+x2=-$\frac{b}{a}$=k-1,x1•x2=$\frac{c}{a}$=k+1,
∵两个实数根满足关系式|x1-x2|=$\sqrt{13}$,
∴|x1-x2|=$\sqrt{({x}_{1+}{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{(k-1)^{2}-4(k+1)}$=$\sqrt{13}$,
∴(k-1)2-4k-4=13,
解得:k=8或-2,
故答案为:8或-2.
点评 此题主要考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
相关题目
6.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
11.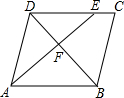 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )| A. | 3:4 | B. | 9:16 | C. | 4:9 | D. | 1:3 |
1.已知m,n是一元二次方程x2-4x-3=0的两个实数根,则代数式(m+1)(n+1)的值为( )
| A. | -6 | B. | -2 | C. | 0 | D. | 2 |
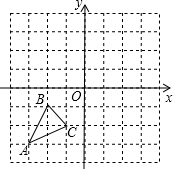 如图,已知A(-3,-3),B(-2,-1),C(-1.-2)是坐标平面上三点.
如图,已知A(-3,-3),B(-2,-1),C(-1.-2)是坐标平面上三点.