题目内容
3. 数学实验室:
数学实验室:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.
利用数形结合思想回答下列问题:
①数轴上表示2和5两点之间的距离是3;
②数轴上表示x和-2的两点之间的距离表示为|x+2|;
③若x表示一个有理数,且-3<x<1,则$|\begin{array}{l}{x-1}\end{array}|+|\begin{array}{l}{x+3}\end{array}|$=4;
④若x表示一个有理数,且$|\begin{array}{l}{x-1}\end{array}|+|\begin{array}{l}{x+3}\end{array}|$>4,则有理数x的取值范围是x<-3或x>1.
分析 ①②在数轴上A、B两点之间的距离AB=|a-b|,依此即可求解;
③根据绝对值的性质去掉绝对值号,然后计算即可得解;
④将x的位置分三种情况讨论,可得出x的取值范围.
解答 解:①数轴上表示2和5两点之间的距离是|5-2|=3;
②根据绝对值的定义有:数轴上表示x和-2的两点之间的距离表示为|x-(-2)|=|x+2|或|-2-x|=|x+2|;
③∵-3<x<-1
∴x+(-1)=x-1<0,x-(-3)=x+3>0
∴$|\begin{array}{l}{x-1}\end{array}|+|\begin{array}{l}{x+3}\end{array}|$=1-x+x+3=4;
④∵当x<-3时,|x-1|+|x+3|=1-x-x-3=-2x-2,
当-3≤x≤1时,|x-1|+|x+3|=1-x+x+3=4,
当x>1时,|x-1|+|x+3|=x-1+x+3=2x+2
∴$|\begin{array}{l}{x-1}\end{array}|+|\begin{array}{l}{x+3}\end{array}|$>4,则有理数x的取值范围是:x<-3或x>1.
故答案为:①3;②|x+2|;③4;④x<-3或x>1.
点评 本题考查了数轴和绝对值的性质,读懂题目信息,理解数轴上两点间的距离的表示方法是解题的关键,数轴上两点间的距离等于两数差的绝对值.注意分类思想的运用.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
8. 如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数为( )
如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数为( )
 如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数为( )
如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数为( )| A. | 75° | B. | 80° | C. | 85° | D. | 90° |
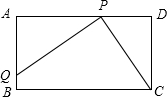 如图,在长方形ABCD中,AD=8,CD=4,P是AD上一点,且PA=PC.
如图,在长方形ABCD中,AD=8,CD=4,P是AD上一点,且PA=PC.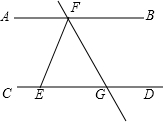 如图,AB∥CD,∠EFB=2∠DEF,FG平分∠EFB,则∠EGF=60°.
如图,AB∥CD,∠EFB=2∠DEF,FG平分∠EFB,则∠EGF=60°.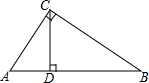 如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm,求:(1)△ABC的面积;(2)CD的长.
如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm,求:(1)△ABC的面积;(2)CD的长.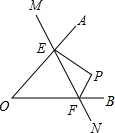 如图,点P在∠AOB内,M、N分别是点P关于AO、BO的对称点,MN分别交AO,BO于点E、F,若△PEF的周长等于20cm,求MN的长.
如图,点P在∠AOB内,M、N分别是点P关于AO、BO的对称点,MN分别交AO,BO于点E、F,若△PEF的周长等于20cm,求MN的长.