题目内容
15.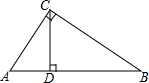 如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm,求:(1)△ABC的面积;(2)CD的长.
如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm,求:(1)△ABC的面积;(2)CD的长.
分析 (1)如图,首先证明△ABC为直角三角形,运用三角形的面积公式即可解决问题.
(2)根据同一个三角形面积的不变性,借助三角形的面积公式列出关于CD的等式,求出CD即可解决问题.
解答  解:(1)如图,在△ABC中,
解:(1)如图,在△ABC中,
∵62+82=102,
∴△ABC为直角三角形,
∴${S}_{△ABC}=\frac{1}{2}×6×8$=24.
(2)∵CD是AB边上的高,
∴$\frac{1}{2}AC•BC=\frac{1}{2}AB•CD$,
∴CD=4.8.
点评 该题主要考查了勾股定理、三角形的面积公式及其应用问题;解题的方法是运用勾股定理首先证明△ABC为直角三角形;解题的关键是灵活运用三角形的面积公式来解答.

练习册系列答案
相关题目
4.下面不是同类项的是( )
| A. | -2与$\frac{1}{2}$ | B. | 2m与2n | C. | -2a2b与a2b | D. | -x2y3与$\frac{1}{2}$x2y3 |
 如图是七个棱长为1的立方块组成的一个几何体,画出其三视图并计算其表面积.
如图是七个棱长为1的立方块组成的一个几何体,画出其三视图并计算其表面积. 数学实验室:
数学实验室: 已知:如图所示,AD是△ABC的高,E为AD上一点,且BE=EC,求证:△ABC是等腰三角形.
已知:如图所示,AD是△ABC的高,E为AD上一点,且BE=EC,求证:△ABC是等腰三角形.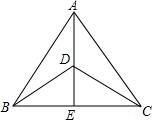 如图,在△ABC中,AB=AC,在BC上取一点E,连接AE,在AE上取一点D,连接BD、CD.若BD=CD,BE=4,则BC的长度为8.
如图,在△ABC中,AB=AC,在BC上取一点E,连接AE,在AE上取一点D,连接BD、CD.若BD=CD,BE=4,则BC的长度为8.