题目内容
14.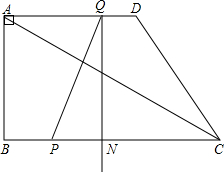 如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=4,BC=7,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D 出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=4,BC=7,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D 出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.(1)求NC、PN的长(用t的代数式表示);
(2)当t为何值时,四边形PCDQ构成平行四边形;
(3)当t为何值时,四边形PCDQ构成等腰梯形?
(4)是否存在某一时刻,使射线QN恰好将梯形ABCD的面积和周长同时平分?若存在,求出此时t的值;若不存在,请说明理由.
分析 (1)首先判定四边形ABNQ是矩形,得出BN=AQ=4-t,则NC=BC-BN=7-(4-t)=t+3,PN=BN-BP=(4-t)-t=4-2t;
(2)因为四边形PCDQ是平行四边形,得出QD=CP,由此建立关于t的方程求得答案即可;
(3)因为四边形PCDQ构成等腰梯形,得出QP=CD,且QD≠CP,由勾股定理分别求得QP和CD,进一步建立方程求得答案即可;
(4)分别由射线QN恰好将梯形ABCD的面积平分和射线QN恰好将梯形ABCD的周长平分建立方程求得t的数值,如果t的值相等,则存在,否则就不存在.
解答 解:(1)∵AD∥BC,∠ABC=90°,QN⊥BC,
∴四边形ABNQ是矩形,
∴BN=AQ=4-t,NC=BC-BN=7-(4-t)=t+3,PN=BN-BP=(4-t)-t=4-2t;
(2)∵四边形PCDQ是平行四边形,
∴QD∥CP,QD=CP,
∴t=7-t,
解得:t=3.5,
即当t=3.5时,四边形PCDQ构成平行四边形;
(3)∵四边形PCDQ构成等腰梯形,
∴QP=CD,且QD≠CP,
∴PN2+QN2=QN2+(BC-AD)2=4+(7-4)2=25,
即(4-2t)2+42=25,
解得:t=0.5或t=3.5(这时QD=CP,不合题意,舍去)
所以当t=0.5时,四边形PCDQ构成等腰梯形;
(4)不存在.
理由:当射线QN恰好将梯形ABCD的面积平分时,
AB•BN=$\frac{1}{2}$(QD+CN)•AB,
即4-t=$\frac{1}{2}$×(t+3)
解得:t=$\frac{5}{3}$,
当射线QN恰好将梯形ABCD的周长平分时,
2(AB+BN)=NC+CD+DQ+QN,
即2(4+4-t)=t+3+5+t+4,
解得:t=1,
两个数值不相等,所以不存在某一时刻,使射线QN恰好将梯形ABCD的面积和周长同时平分.
点评 此题综合考查了梯形的性质,矩形的判定与性质,等腰梯形的判定与性质,平行四边形的判定与性质,勾股定理的运用,掌握基本性质定理是解决问题的关键.

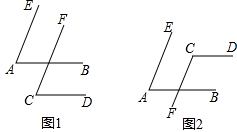
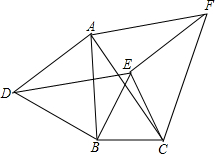 如图,以△ABC三边为边在BC的同一侧分别作3个等边三角形,即△ABD、△BCE、△ACF.四边形AFED一定是平行四边形吗?如果是,请说明理由.
如图,以△ABC三边为边在BC的同一侧分别作3个等边三角形,即△ABD、△BCE、△ACF.四边形AFED一定是平行四边形吗?如果是,请说明理由.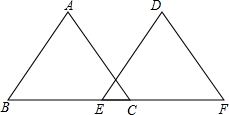 如图:B、E、C、F四点在同一直线上,且∠ACB=∠F,∠B=∠DEF,BE=CF,∠A=50°,求∠D的度数,并说明理由.
如图:B、E、C、F四点在同一直线上,且∠ACB=∠F,∠B=∠DEF,BE=CF,∠A=50°,求∠D的度数,并说明理由.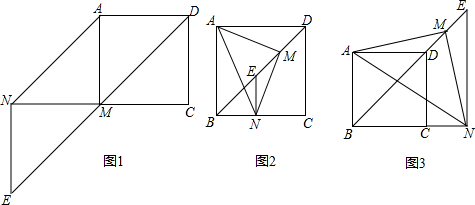
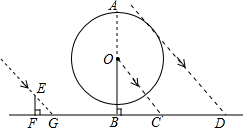 同一时刻甲、乙两组同学在阳光下进行测量,甲组将一根长为2.4m的竹竿EF直立于平地,测得竹竿的影长FG为1.8m;摩天轮的立柱OB直立于平地,乙组测得立柱OB的影长BC为36m,摩天轮在立柱右侧影子的边缘D与立柱OB相距86m,求摩天轮的半径和最高点A的高.
同一时刻甲、乙两组同学在阳光下进行测量,甲组将一根长为2.4m的竹竿EF直立于平地,测得竹竿的影长FG为1.8m;摩天轮的立柱OB直立于平地,乙组测得立柱OB的影长BC为36m,摩天轮在立柱右侧影子的边缘D与立柱OB相距86m,求摩天轮的半径和最高点A的高.