题目内容
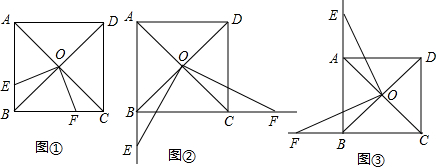
9. 如图,以△ABC三边为边在BC的同一侧分别作3个等边三角形,即△ABD、△BCE、△ACF.四边形AFED一定是平行四边形吗?如果是,请说明理由.
如图,以△ABC三边为边在BC的同一侧分别作3个等边三角形,即△ABD、△BCE、△ACF.四边形AFED一定是平行四边形吗?如果是,请说明理由.
分析 首先得出△ABC≌△FEC,推出AD=FE,同理求出△ABC≌DBE,推出ED=AF,根据平行四边形的判定推出即可.
解答 证明:∵△ABD、△BCE、△ACF为等边三角形
∴CB=CE,CA=CF,∠BCE=∠ACF=60°,
∴∠BCE-∠ACE=∠ACF-∠ACE,
即∠BCA=∠ECF,
在△ABC和△FEC中
∵$\left\{\begin{array}{l}{BC=CE}\\{∠ACB=∠FCE}\\{CA=CF}\end{array}\right.$,
∴△ABC≌△FEC(SAS),
∴AB=EF,
又∵AB=AD,
∴AD=FE,
同理可证△ABC≌△DBE,ED=FA,
∴四边形AFED是平行四边形.
点评 本题考查了全等三角形的旋转和判定、等边三角形的性质,平行四边形的判定等知识点的应用,主要是证△ABC≌△FEC和△ABC≌△DBE,题型较好,是一道综合性比较强的题目.

练习册系列答案
相关题目
17.点P是直线l外一点,A为垂足,且PA=4cm,则点P到直线l的距离( )
| A. | 小于4cm | B. | 等于4cm | C. | 大于4cm | D. | 不确定 |
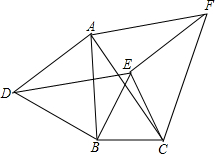
 如图,一个六边形的六个内角都是120°,AB=1,BC=CD=3,DE=2,求该六边形的周长.
如图,一个六边形的六个内角都是120°,AB=1,BC=CD=3,DE=2,求该六边形的周长.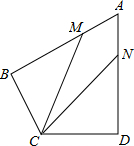 如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则∠BCD=120°,cos∠MCN=$\frac{13}{14}$.
如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则∠BCD=120°,cos∠MCN=$\frac{13}{14}$.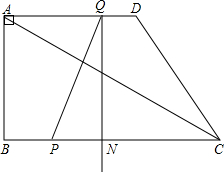 如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=4,BC=7,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D 出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=4,BC=7,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D 出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.