题目内容
18.(1)解不等式:1+$\frac{x}{3}$>5-$\frac{x-2}{2}$;(2)解不等式组:$\left\{\begin{array}{l}{\frac{x}{2}≥-1}\\{2x+1>5(x-1)}\end{array}\right.$,并写出它的所有整数解.
分析 (1)去分母,去括号,移项,合并同类项,系数化成1即可;
(2)先求出每个不等式的解集,再根据不等式的解集找出不等式组的解集即可.
解答 解:(1)去分母得:6+2x>30-3(x-2),
6+2x>30-3x+6,
2x+3x>30+6-6,
5x>30,
x>6;
(2)$\left\{\begin{array}{l}{\frac{x}{2}≥-1①}\\{2x+1>5(x-1)②}\end{array}\right.$
∵解不等式①得:x≥-2,
解不等式②得:x<2,
∴不等式组的解集为:-2≤x<2,
∴不等式组的整数解为-2,-1,0,1.
点评 本题考查了解一元一次不等式,解一元一次不等式组,不等式组的整数解的应用,能正确运用不等式的性质求出不等式或不等式组的解集是解此题的关键,难度适中.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
3.下列说法中错误的是( )
| A. | 成轴对称的两个图形的对应点连线的垂直平分线是它们的对称轴 | |
| B. | 关于某条直线对称的两个图形全等 | |
| C. | 若两个图形沿某条直线对折后能够完全重合,我们称两个图形成轴对称 | |
| D. | 全等的三角形一定关于某条直线对称 |
 一平面镜以与水平面成45°角固定在水平面上,如图所示,一小球以1米/秒的速度沿桌面向平面镜匀速滚去,则小球在平面镜里所成的像将竖直向下.
一平面镜以与水平面成45°角固定在水平面上,如图所示,一小球以1米/秒的速度沿桌面向平面镜匀速滚去,则小球在平面镜里所成的像将竖直向下. 如图,在?ABCD中,已知AB=$\sqrt{3}$,BC=$\sqrt{7}$,∠BAC=90°,求OB的长.
如图,在?ABCD中,已知AB=$\sqrt{3}$,BC=$\sqrt{7}$,∠BAC=90°,求OB的长.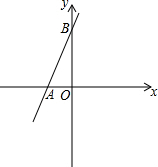 如图,直线y=2x+4与x轴相交于点A,与y轴相交于点B.
如图,直线y=2x+4与x轴相交于点A,与y轴相交于点B.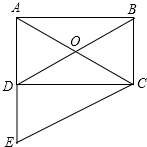 如图所示,在矩形ABCD中,对角线AC、BD相交于点O,CE∥DB,交AD的延长线于点E.
如图所示,在矩形ABCD中,对角线AC、BD相交于点O,CE∥DB,交AD的延长线于点E.