题目内容
5.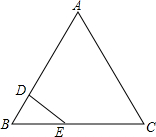 如图,等边△ABC的边长为4cm,点D从B点出发,沿BA方向运动到点A,到点A停止运动,点E从B点出发,沿BC方向运动,点D,E的速度分别为1cm/s,2cm/s,它们同时出发且同时停止,设它们运动的时间为t秒.
如图,等边△ABC的边长为4cm,点D从B点出发,沿BA方向运动到点A,到点A停止运动,点E从B点出发,沿BC方向运动,点D,E的速度分别为1cm/s,2cm/s,它们同时出发且同时停止,设它们运动的时间为t秒.(1)求证:以E为圆心,以DE为半径的圆与直线AB相切;
(2)当时间t为何值时,以E为圆心,以DE为半径的圆与直线AC相切?
分析 (1)过点D作DM⊥AC于点M,由△ABC为等边三角形,得出∠B=60°,可得BM=$\frac{1}{2}$t,DM=$\frac{\sqrt{3}}{2}$t,再求得BE与ME的长,则可得在△BDE中,BD2+DE2=BE2,由勾股定理的逆定理得出∠BDE=90°,即可得出AB与⊙D相切;
(2)作EF⊥AC于F,连接AE,由切线长定理可得AE平分∠BAC,然后由等边三角形的性质,求得BE的长,即可得出结果;
解答 (1)证明:过点D作DM⊥BC于点M,如图1所示: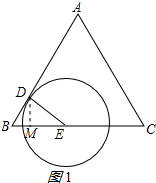
∵△ABC为等边三角形,
∴∠B=60°,
在Rt△BDM中,
∵BD=t,∠B=60°,
∴BM=$\frac{1}{2}$t,DM=$\frac{\sqrt{3}}{2}$t,
∵BE=2t,∴ME=$\frac{3}{2}$t,在Rt△DME中,DE2=DM2+ME2=3t2,在△BDE中,∵BD2=t2,BE2=4t2,DE2=3t2,∴BD2+DE2=BE2,∴∠BDE=90°,∴AB与⊙E相切;
(2)解:作EF⊥AC于F,连接AE,如图2所示: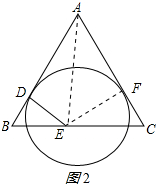 ∵AB、AC与⊙O相切,
∵AB、AC与⊙O相切,
∴AE平分∠BAC,
∵AB=AC,
∴BE=CE,
∵BC=4,
∴BE=2,
∴t=1;
即t=1s时,以E为圆心,以DE为半径的圆与直线AC相切.
点评 此题考查了切线的性质与判定、勾股定理以及逆定理、圆与圆的位置关系切线长定理等知识;此题难度较大,注意掌握辅助线的作法,注意数形结合思想与分类讨论思想的应用.

练习册系列答案
相关题目
16.若∠1=15°12′,∠2=15.3°,∠3=15°18′,则( )
| A. | ∠1=∠2 | B. | ∠1=∠3 | C. | ∠2=∠3 | D. | 以上均不对 |
17.若某数的平方根是a+3和2a-15,则这个数是( )
| A. | 49 | B. | 4 | C. | 18 | D. | 3 |
14.下列二次根式中是最简二次根式的个数有( )
$\sqrt{0.5}$,$\sqrt{5}$,$\sqrt{50}$,$\sqrt{{a}^{2}b}$(b>0),$\sqrt{25}$.
$\sqrt{0.5}$,$\sqrt{5}$,$\sqrt{50}$,$\sqrt{{a}^{2}b}$(b>0),$\sqrt{25}$.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
15.方程2x2-$\sqrt{5}$x-3=0的两根是( )
| A. | x=$\frac{\sqrt{5}±\sqrt{11}}{2}$ | B. | x=$\frac{\sqrt{5}±\sqrt{29}}{4}$ | C. | x=$\frac{-\sqrt{5}±\sqrt{29}}{2}$ | D. | x=$\frac{-\sqrt{5}±\sqrt{29}}{4}$ |
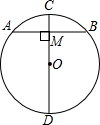 如图.在下列五个条件中:①CD是直径,②CD⊥AB,③AM=BM,④$\widehat{AC}=\widehat{BC}$,③$\widehat{AD}=\widehat{BD}$,只要具备其中两个条件,就可推出其余三个结论.你可以写出相应的命题吗?
如图.在下列五个条件中:①CD是直径,②CD⊥AB,③AM=BM,④$\widehat{AC}=\widehat{BC}$,③$\widehat{AD}=\widehat{BD}$,只要具备其中两个条件,就可推出其余三个结论.你可以写出相应的命题吗?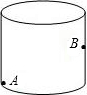 有一圆柱形食品盒,它的高等于8cm,底面直径为$\frac{18}{π}$cm,蚂蚁爬行的速度为2cm/s.如果在盒内下底面的A处有一只蚂蚁,它想吃到盒内对面中部点B处的食物,那么它至少需要多少时间?(盒的厚度和蚂蚁的大小忽略不计,结果可含根号)
有一圆柱形食品盒,它的高等于8cm,底面直径为$\frac{18}{π}$cm,蚂蚁爬行的速度为2cm/s.如果在盒内下底面的A处有一只蚂蚁,它想吃到盒内对面中部点B处的食物,那么它至少需要多少时间?(盒的厚度和蚂蚁的大小忽略不计,结果可含根号)