题目内容
20．
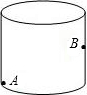有一圆柱形食品盒，它的高等于8cm，底面直径为$\frac{18}{π}$cm，蚂蚁爬行的速度为2cm/s．如果在盒内下底面的A处有一只蚂蚁，它想吃到盒内对面中部点B处的食物，那么它至少需要多少时间？（盒的厚度和蚂蚁的大小忽略不计，结果可含根号）
分析 把圆柱的侧面展开，再利用勾股定理求解即可．
解答 
解：如图，AC=π•$\frac{18}{π}$÷2=9cm，BC=4cm，则蚂蚁走过的最短路径为：AB=$\sqrt{{9}^{2}+{4}^{2}}$=$\sqrt{97}$cm，
所用时间为：$\sqrt{97}$÷2=$\frac{\sqrt{97}}{2}$（秒）．
点评 本题考查的是平面展开-最短路径问题，根据题意画出圆柱的侧面展开图，利用勾股定理求解是解答此题的关键．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
如图是一套小户型经济房子的平面图尺寸
15．下列各式中，正确的是（ ）
| A． | $\sqrt{25}$=±5 | B． | $\sqrt{（-5）^{2}}$=5 | C． | $\sqrt{16\frac{1}{4}}$=4$\frac{1}{2}$ | D． | $\root{3}{-8}$=2 |
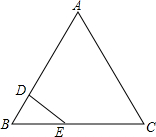如图，等边△ABC的边长为4cm，点D从B点出发，沿BA方向运动到点A，到点A停止运动，点E从B点出发，沿BC方向运动，点D，E的速度分别为1cm/s，2cm/s，它们同时出发且同时停止，设它们运动的时间为t秒．
12．点P（1，-3）所在的象限是（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |