题目内容
20.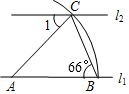 如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC,若∠ABC=66°,则∠1=( )
如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC,若∠ABC=66°,则∠1=( )| A. | 23° | B. | 46° | C. | 66° | D. | 48° |
分析 首先由题意可得:AB=AC,根据等边对等角的性质,可求得∠ACB的度数,又由直线l1∥l2,根据两直线平行,同旁内角互补即可求得∠1的度数.
解答 解:根据题意得:AB=AC,
∴∠ACB=∠ABC=66°,
∵直线l1∥l2,
∴∠1+∠ACB+∠ABC=180°,
∴∠1=180°-∠ABC-∠ACB=180°-66°-66°=48°.
故选D.
点评 此题考查了平行线的性质,等腰三角形的性质.此题难度不大,解题的关键是注意掌握两直线平行,同旁内角互补与等边对等角定理的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.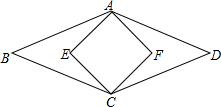 如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为( )
如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为( )
 如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为( )
如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为( )| A. | 10cm | B. | 13cm | C. | 15cm | D. | 24cm |
11.下列各题合并同类项的结果正确的是( )
| A. | 2x+4x=8x2 | B. | 3x+2y=5xy | C. | 7x2-3x2=4 | D. | 9a2b-9ba2=0 |
8. 如图,在矩形ABCD中,AB=6,BC=8,现要在该矩形中作出面积最大的菱形,则菱形的边长为( )
如图,在矩形ABCD中,AB=6,BC=8,现要在该矩形中作出面积最大的菱形,则菱形的边长为( )
 如图,在矩形ABCD中,AB=6,BC=8,现要在该矩形中作出面积最大的菱形,则菱形的边长为( )
如图,在矩形ABCD中,AB=6,BC=8,现要在该矩形中作出面积最大的菱形,则菱形的边长为( )| A. | 5 | B. | 6 | C. | $\frac{25}{4}$ | D. | $\frac{27}{4}$ |
5.我县某乡镇冬枣园2014年产量为1000吨,2016年产量为1440吨,求该冬枣园冬枣产量的年平均增长率,设该冬枣园冬枣产量的年平均增长量为x,则根据题意可列方程为( )
| A. | 1440(1-x)2=1000 | B. | 1000(1-x)2=1440 | C. | 1440(1+x)2=1000 | D. | 1000(1+x)2=1440 |
12.去年我县12月份某天的最低气温为-6℃,最高气温为-2℃,那么这一天的最高气温比最低气温高( )
| A. | 4℃ | B. | -4℃ | C. | 8℃ | D. | -8℃ |
17.一个水池有甲、乙两个水龙头,单独开甲水龙头2小时可把空池灌满;单独开乙水龙头3小时可把空池灌满,若同时开放两个水龙头,灌满水池需( )
| A. | $\frac{6}{5}$小时 | B. | $\frac{5}{6}$小时 | C. | 2小时 | D. | 3小时 |
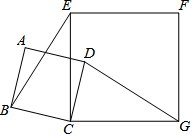 如图,在正方形ABCD和正方形ECGF中,连接BE,DG.求证:BE=DG.
如图,在正方形ABCD和正方形ECGF中,连接BE,DG.求证:BE=DG.