题目内容
8. 如图,在矩形ABCD中,AB=6,BC=8,现要在该矩形中作出面积最大的菱形,则菱形的边长为( )
如图,在矩形ABCD中,AB=6,BC=8,现要在该矩形中作出面积最大的菱形,则菱形的边长为( )| A. | 5 | B. | 6 | C. | $\frac{25}{4}$ | D. | $\frac{27}{4}$ |
分析 根据折叠的性质得到EF垂直平分AC,得出四边形AFCE是菱形,OA=OC,∠AOF=90°,则FA=FC,设AF=x,则FC=x,BF=BC-x=8-x,在Rt△ABF中根据勾股定理可计算出x即可.
解答 解:如图所示: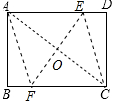
∵矩形折叠后点C与点A重合,
∴EF垂直平分AC,
则四边形AFCE是菱形,OA=OC,∠AOF=90°,
∴FA=FC,
设AF=x,则FC=x,BF=BC-x=8-x,
在Rt△ABF中,AB2+BF2=AF2,即62+(8-x)2=x2,
解得x=$\frac{25}{4}$;
故选:C.
点评 本题考查折叠的性质:折叠前后两图形全等,即对应线段相等,对应角相等;对应点的连线段被折痕垂直平分.也考查了矩形的性质以及勾股定理.

练习册系列答案
相关题目
18.顺次连结任意四边形各边中点所得的四边形一定是( )
| A. | 正方形 | B. | 菱形 | C. | 平行四边形 | D. | 矩形 |
19.下列叙述,正确的是( )
| A. | 两个等腰三角形一定相似 | B. | 两个矩形一定相似 | ||
| C. | 两个菱形一定相似 | D. | 两个正方形一定相似 |
16.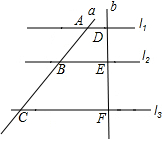 如图,直线l1∥l2∥l3,且分别交直线a,b于点A、B、C、D、E、F,若AB=2,BC=3,DE=1,则EF的长为( )
如图,直线l1∥l2∥l3,且分别交直线a,b于点A、B、C、D、E、F,若AB=2,BC=3,DE=1,则EF的长为( )
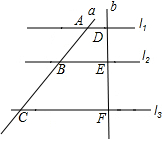 如图,直线l1∥l2∥l3,且分别交直线a,b于点A、B、C、D、E、F,若AB=2,BC=3,DE=1,则EF的长为( )
如图,直线l1∥l2∥l3,且分别交直线a,b于点A、B、C、D、E、F,若AB=2,BC=3,DE=1,则EF的长为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | 6 | D. | $\frac{1}{6}$ |
3.在一个不透明的盒子中,装有4个黑球和若干个白球,它们除颜色外没有任何其他区别,摇匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复以上操作过程,共摸了100次球,发现有20次摸到黑球,据此估计盒子中白球的个数为( )
| A. | 12个 | B. | 16个 | C. | 20个 | D. | 30个 |
13.某款服装按原售价提价a元后,再降价20%,现在售价为b元,则原售价为( )
| A. | ($\frac{5}{4}$b+a)元 | B. | ($\frac{5}{4}$b+a)元 | C. | (a+b)元 | D. | ($\frac{5}{4}$a+b)元 |
20.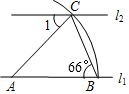 如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC,若∠ABC=66°,则∠1=( )
如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC,若∠ABC=66°,则∠1=( )
 如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC,若∠ABC=66°,则∠1=( )
如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC,若∠ABC=66°,则∠1=( )| A. | 23° | B. | 46° | C. | 66° | D. | 48° |
 如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是4$\sqrt{5}$.
如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是4$\sqrt{5}$.