题目内容
9.(1)解方程:$\frac{1}{9x-3}$=$\frac{1}{3}$-$\frac{2}{1-3x}$;(2)求不等式组$\left\{\begin{array}{l}{x+1>2}\\{3x-1≤x+5}\end{array}\right.$的整数解.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分确定出不等式组的解集,进而求出不等式组的整数解即可.
解答 解:(1)去分母得:1=3x-1+6,
解得:x=-$\frac{4}{3}$,
经检验x=-$\frac{4}{3}$是分式方程的解;
(2)$\left\{\begin{array}{l}{x+1>2①}\\{3x-1<x+5②}\end{array}\right.$,
由①得:x>1,
由②得:x<3,
∴不等式组的解集为1<x<3,
则不等式组的整数解为2.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.

练习册系列答案
相关题目
11. 图中立体图形的主视图是( )
图中立体图形的主视图是( )
 图中立体图形的主视图是( )
图中立体图形的主视图是( )| A. |  | B. |  | C. |  | D. |  |
4. 如图,AB∥CD,AD=CD,∠2=40°,则∠1的度数是( )
如图,AB∥CD,AD=CD,∠2=40°,则∠1的度数是( )
 如图,AB∥CD,AD=CD,∠2=40°,则∠1的度数是( )
如图,AB∥CD,AD=CD,∠2=40°,则∠1的度数是( )| A. | 80° | B. | 75° | C. | 70° | D. | 65° |
18.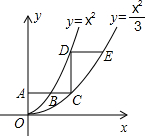 如图,平行于x轴的直线AC分别交抛物线y1=x2与y2=$\frac{x^2}{3}$于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC交y2于点E,则$\frac{DE}{AB}$的值是( )
如图,平行于x轴的直线AC分别交抛物线y1=x2与y2=$\frac{x^2}{3}$于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC交y2于点E,则$\frac{DE}{AB}$的值是( )
 如图,平行于x轴的直线AC分别交抛物线y1=x2与y2=$\frac{x^2}{3}$于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC交y2于点E,则$\frac{DE}{AB}$的值是( )
如图,平行于x轴的直线AC分别交抛物线y1=x2与y2=$\frac{x^2}{3}$于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC交y2于点E,则$\frac{DE}{AB}$的值是( )| A. | 2 | B. | y=$\frac{3}{2}$ | C. | 3-$\sqrt{2}$ | D. | 3-$\sqrt{3}$ |
19.今年1~2月,我市完成固定资产投资201.4亿元,增速21%,高于全省平均增速8.6个百分点,增速继续保持全省第一,数据201.4亿用科学记数法表示为( )
| A. | 201.4×108 | B. | 2.014×108 | C. | 2.014×109 | D. | 2.014×1010 |
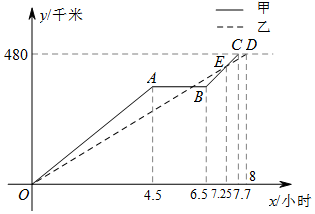 重阳节期间,某单位组织本单位退休职工前去距离商丘480千米的信阳鸡公山登高旅游,由于人数较多,共租用甲、乙两辆长途汽车沿同一路线赶赴景点.图中的折线、线段分别表示甲、乙两车所走的路程y甲(千米),y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
重阳节期间,某单位组织本单位退休职工前去距离商丘480千米的信阳鸡公山登高旅游,由于人数较多,共租用甲、乙两辆长途汽车沿同一路线赶赴景点.图中的折线、线段分别表示甲、乙两车所走的路程y甲(千米),y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题: