题目内容
7.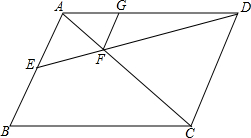 如图,?ABCD中,AB=6,E为AB中点,DE交AC于点F,FG∥AB交AD于点G,求线段FG的长.
如图,?ABCD中,AB=6,E为AB中点,DE交AC于点F,FG∥AB交AD于点G,求线段FG的长.
分析 由平行四边形的性质可求得$\frac{DF}{EF}$=$\frac{DC}{AE}$,再根据平行线分线段成比例可得$\frac{FG}{AE}$=$\frac{DF}{DE}$,可求得FG.
解答 解:∵四边形ABCD为平行四边形,
∴AB=CD=6,
∵E为AB中点,
∴AE=3,
∵AB∥CD,
∴$\frac{DF}{EF}$=$\frac{DC}{AE}$=$\frac{6}{3}$=2,
∴$\frac{DF}{DE}$=$\frac{2}{3}$,
∵FG∥AB,
∴$\frac{FG}{AE}$=$\frac{DF}{DE}$=$\frac{2}{3}$,即$\frac{FG}{3}$=$\frac{2}{3}$,解得FG=2,
∴线段FG长为2.
点评 本题主要考查平行线分线段成比例,掌握平行线分所分线段对应成比例是解题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
20.已知关于x的方程5(x-a)=-2a的根大于关于x的方程3(x-a)=2(x+a)的根,则a应是( )
| A. | 不为0的数 | B. | 正数 | C. | 负数 | D. | 大于-1的数 |
12.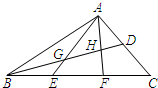 如图,在△ABC中,AD=DC,BE=EF=FC,AE、AF与BD相交于点G、H.已知${S_{△AHD}}=\frac{3}{10}$,则S四边形GEFH的值是( )
如图,在△ABC中,AD=DC,BE=EF=FC,AE、AF与BD相交于点G、H.已知${S_{△AHD}}=\frac{3}{10}$,则S四边形GEFH的值是( )
 如图,在△ABC中,AD=DC,BE=EF=FC,AE、AF与BD相交于点G、H.已知${S_{△AHD}}=\frac{3}{10}$,则S四边形GEFH的值是( )
如图,在△ABC中,AD=DC,BE=EF=FC,AE、AF与BD相交于点G、H.已知${S_{△AHD}}=\frac{3}{10}$,则S四边形GEFH的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{7}{10}$ | C. | $\frac{6}{11}$ | D. | $\frac{11}{20}$ |
19.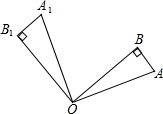 如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )
如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )
 如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )
如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )| A. | 125° | B. | 65° | C. | 75° | D. | 50° |
17.下面是石林县某校八年级(1)班七位女同学的体重(单位:kg):51 50 40 43 48 48 63,这组数据的众数和中位数分别是( )
| A. | 48,43 | B. | 48,48 | C. | 43,48 | D. | 48,49 |
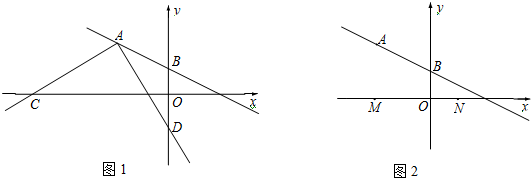
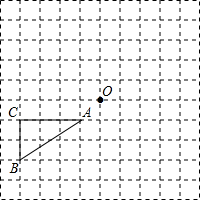 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有△ABC.点A、B、C、O均在小正方形的顶点上.
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有△ABC.点A、B、C、O均在小正方形的顶点上. 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°.
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°.