题目内容
2.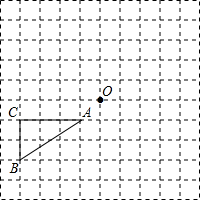 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有△ABC.点A、B、C、O均在小正方形的顶点上.
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有△ABC.点A、B、C、O均在小正方形的顶点上.(1)在方格纸中画△A1B1C1,使△A1B1C1与△ABC关于点O对称;
(2)连接AB1直接写出线段AB1的长.
分析 (1)首先在方格纸中画出点A、B、C关于点O的对称点A1、B1、C1,然后顺次连接,即可得到△A1B1C1与△ABC关于点O对称.
(2)首先延长CA交B1C1的延长线于点D,然后在直角三角形ADB1中,根据勾股定理,求出线段AB1的长是多少即可.
解答 解:(1)如图1,根据分析,可得 .
.
(2)如图2,延长CA交B1C1的延长线于点D, ,
,
AB1=$\sqrt{{AD}^{2}{{+DB}_{1}}^{2}}$=$\sqrt{{5}^{2}{+4}^{2}}=\sqrt{41}$,
∴线段AB1的长是$\sqrt{41}$.
点评 此题主要考查了作图-旋转变换问题,要熟练掌握,解答此题的关键是要明确旋转图形的作法:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
相关题目
 如图,∠AOC=∠BOD=110°,若∠AOB=150°,∠COD=m°,则m=70.
如图,∠AOC=∠BOD=110°,若∠AOB=150°,∠COD=m°,则m=70. 如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.
如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.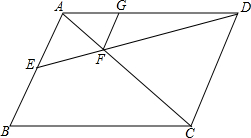 如图,?ABCD中,AB=6,E为AB中点,DE交AC于点F,FG∥AB交AD于点G,求线段FG的长.
如图,?ABCD中,AB=6,E为AB中点,DE交AC于点F,FG∥AB交AD于点G,求线段FG的长.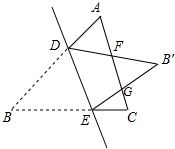 已知△ABC中,AC=BC,点D、E分别在边AB、AC上,把△BDE沿直线DE翻折,使点B落在B′处,DB′,EB′分别交AC于点F、G,若∠ADF=80°,则∠EGC的大小为( )
已知△ABC中,AC=BC,点D、E分别在边AB、AC上,把△BDE沿直线DE翻折,使点B落在B′处,DB′,EB′分别交AC于点F、G,若∠ADF=80°,则∠EGC的大小为( ) 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=30°.
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=30°.