题目内容
13.△ABC中,点B和点C分别在AD,AE上,且AB=2BD,AC=2BD,AC=2CE,则BC:DE=2:3.分析 根据题意得到$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{2}{3}$,根据相似三角形的判定定理得到△ABC∽△ADE,根据相似三角形的性质定理得到答案.
解答 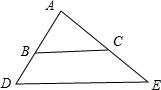 解:∵AB=2BD,AC=2CE,
解:∵AB=2BD,AC=2CE,
∴$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{2}{3}$,∠A=∠A,
∴△ABC∽△ADE,
∴$\frac{BC}{DE}$=$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{2}{3}$,
故答案为:2:3.
点评 本题考查的是相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
8.若一个三角形的三个内角互不相等,则它的最小角必小于( )
| A. | 45° | B. | 60° | C. | 30° | D. | 90° |
17.某玩具厂广告称:“本厂工人工作时间为每天工作8小时,每月工作25天;待遇是熟练工人按时计件付工资,多劳多得,计件工资每月下来不少于900元,每月另加福利工资100元,按月结算…”该厂只生产两种玩具:小狗和小汽车,熟练工人晓云元月份领工资一千多元,她记录了如下表的一些数据:
(1)制作一个小狗和一辆小汽车各需要多少时间?
(2)制作一个小狗和一辆小汽车的计件工资各是多少元?
(3)假设晓云的工作效率不变,并且按时上下班,若晓云想二月份领工资不少于1115元,那么她二月份至少要生产小汽车多少个?
(4)元月份制作小狗和小汽车的数目没有限制,从二月份开始,厂方从销售方面考虑逐月调整为:k月份每个工人生产的小狗的个数不少于生产的小汽车的个数的k倍(k=2,3,4,…,12),假设晓云的工作效率不变,且服从工厂的安排,请运用所学数学知识说明厂家广告是否有欺诈行为?
| 小狗件数(单位:个) | 小汽车个数(单位:个) | 总时间(单位:分) | 总工资(单位:元) |
| 1 | 1 | 35 | 2.80 |
| 2 | 2 | 70 | 5.60 |
| 3 | 2 | 85 | 6.65 |
(2)制作一个小狗和一辆小汽车的计件工资各是多少元?
(3)假设晓云的工作效率不变,并且按时上下班,若晓云想二月份领工资不少于1115元,那么她二月份至少要生产小汽车多少个?
(4)元月份制作小狗和小汽车的数目没有限制,从二月份开始,厂方从销售方面考虑逐月调整为:k月份每个工人生产的小狗的个数不少于生产的小汽车的个数的k倍(k=2,3,4,…,12),假设晓云的工作效率不变,且服从工厂的安排,请运用所学数学知识说明厂家广告是否有欺诈行为?
 由几个小立方块搭成的几何体从正面和左面看到的图形相同.如图,请你判断一下,最多有多少个小正方体?最少有多少个小正方体?
由几个小立方块搭成的几何体从正面和左面看到的图形相同.如图,请你判断一下,最多有多少个小正方体?最少有多少个小正方体?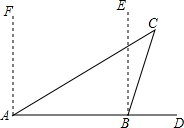 如图,一艘轮船上午8时在A处沿正东方向行驶,在A处测得灯塔C在北偏东60°方向上,行驶1小时后到达B处,在B处测得灯塔C在北偏东20°方向上.求△ABC各内角及∠DBC的度数.
如图,一艘轮船上午8时在A处沿正东方向行驶,在A处测得灯塔C在北偏东60°方向上,行驶1小时后到达B处,在B处测得灯塔C在北偏东20°方向上.求△ABC各内角及∠DBC的度数.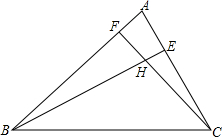 在△ABC中,已知∠ABC=45°,∠ACB=60°,BE是AC上的高,CF交AB于点F,交BE于点H,且∠BHC=105°,△BFH是直角三角形吗?为什么?
在△ABC中,已知∠ABC=45°,∠ACB=60°,BE是AC上的高,CF交AB于点F,交BE于点H,且∠BHC=105°,△BFH是直角三角形吗?为什么? 如图所示.在锐角△ABC中,AD⊥BC于点D,求证:AC2=AB2+BC2-2BC•BD.
如图所示.在锐角△ABC中,AD⊥BC于点D,求证:AC2=AB2+BC2-2BC•BD. 在下列四个三角形中,不能由△ABC经过旋转或平移得到的是( )
在下列四个三角形中,不能由△ABC经过旋转或平移得到的是( )


