题目内容
1．
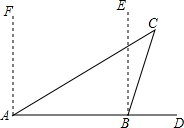如图，一艘轮船上午8时在A处沿正东方向行驶，在A处测得灯塔C在北偏东60°方向上，行驶1小时后到达B处，在B处测得灯塔C在北偏东20°方向上．求△ABC各内角及∠DBC的度数．
分析 根据题意确定∠CAB和∠ABC的度数，根据三角形内角和定理求出∠C的度数，根据邻补角的性质得到∠DBC的度数．
解答 解：∵在A处测得灯塔C在北偏东60°方向上，
∴∠FAC=60°，
∴∠CAB=30°，
∵在B处测得灯塔C在北偏东20°方向上，
∴∠EBC=20°，
∴∠ABC=110°，
则∠C=180°-30°-110°=40°，
∠DBC=180°-∠ABC=70°．
答：∠CAB=30°，∠ABC=110°，∠C=40°，∠DBC=70°．
点评 本题考查的是方向角的计算，掌握三角形内角和定理和邻补角的性质是解题的关键．
练习册系列答案
全能练考卷系列答案
相关题目
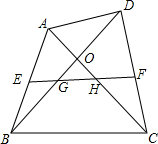如图，在四边形ABCD中，AC与BD交于点O，E为AB中点，F为CD中点，EF分别与BD、AC交于点G、H．
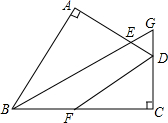如图，四边形ABCD中，∠A=∠C=90°，BE平分∠ABC，DF平分∠ADC，BE、CD交于G点
9．若n边形的所有内角与某一个外角的总和为1297°，则n等于（ ）
| A． | 6 | B． | 7 | C． | 8 | D． | 9 |
6．
如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，则图中相等的锐角有（ ）
如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，则图中相等的锐角有（ ）| A． | 1对 | B． | 2对 | C． | 3对 | D． | 4对 |
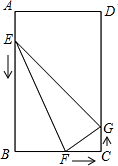如图，在矩形ABCD中，AB=12cm，BC=8cm．点E、F、G分别从点A、B、C同时出发，沿矩形的边按逆时针方向移动，点E、G的速度均为2cm/s，点F的速度为4cm/s，当点F追上点G（即点F与点G重合）时，三个点随之停止移动．设移动开始后第ts时，△EFG的面积为Scm2．
如图，将-4，-3，-2，-1，0，1，2，3，4这9个数字填入图中的9个方格中，使得方格中，每行，每列，以及对角线上的3个数字之和都为0．