题目内容
5. 如图所示.在锐角△ABC中,AD⊥BC于点D,求证:AC2=AB2+BC2-2BC•BD.
如图所示.在锐角△ABC中,AD⊥BC于点D,求证:AC2=AB2+BC2-2BC•BD.
分析 在直角△ABD和直角△ACD中,利用勾股定理分别求得AB2、AC2,然后利用完全平方公式即可证得结论.
解答  解:∵AD⊥BC,BC=BD+CD,
解:∵AD⊥BC,BC=BD+CD,
∴AB2=AD2+BD2,AC2=AD2+CD2,
∴AB2+BC2-2BC•BD=AD2+BD2+(BD+CD)2-2(BD+CD)•BD=AD2+CD2,
∴AC2=AB2+BC2-2BC•BD.
点评 本题考查了勾股定理的应用.解此类题目时,要注意将线段的数量关系转化成直角三角形中相关线段间的数量关系,然后再进行计算.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
15.在下列多项式乘法中,不能用平方差公式计算的是( )
| A. | (a-b)(-a+b) | B. | (m3-n3)(m3+n3) | C. | (-7-x)(7-x) | D. | (x2-y2)(y2+x2) |
8.某校举办初中生演讲比赛,每班派一名学生参赛,现某班有A、B、C三名学生竞选,他们的笔试成绩和口试成绩(单位:分)分别用两种方式进行了统计,如表和图①:
(1)请将表和图1中的空缺部分补充完整;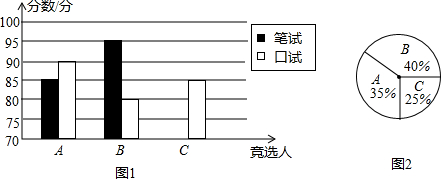
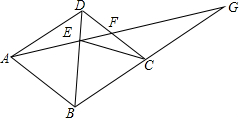
(2)竞选的最后一个程序是由本校的300名学生代表进行投票,每票计1分,三名候选人的得票情况如图2(没有弃权票,每名学生只能推荐一人).
①若将笔试、口试、得票三项测试得分按4:3:3的比例确定最后成绩,请计算学生A的最后成绩;
②若规定得票测试分占20%,要使学生B最后得分不低于91分,则笔试成绩在总分中所占比例的取值范围应是0.2≤x≤0.8.
| A | B | C | |
| 笔试 | 85 | 95 | 90 |
| 口试 | 90 | 80 | 85 |

(2)竞选的最后一个程序是由本校的300名学生代表进行投票,每票计1分,三名候选人的得票情况如图2(没有弃权票,每名学生只能推荐一人).
①若将笔试、口试、得票三项测试得分按4:3:3的比例确定最后成绩,请计算学生A的最后成绩;
②若规定得票测试分占20%,要使学生B最后得分不低于91分,则笔试成绩在总分中所占比例的取值范围应是0.2≤x≤0.8.
 已知四边形ABCD是菱形,G是BC延长线上一点,AG交BD于点E,交CD于点K,若EF=4,FG=5,求CE的长.
已知四边形ABCD是菱形,G是BC延长线上一点,AG交BD于点E,交CD于点K,若EF=4,FG=5,求CE的长.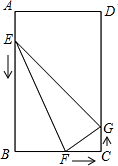 如图,在矩形ABCD中,AB=12cm,BC=8cm.点E、F、G分别从点A、B、C同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第ts时,△EFG的面积为Scm2.
如图,在矩形ABCD中,AB=12cm,BC=8cm.点E、F、G分别从点A、B、C同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第ts时,△EFG的面积为Scm2.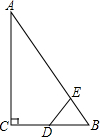 如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,点D为BC的中点,动点E从点A出发,沿着A→B→A的方向以1cm/s的速度运动,当回到点A时停止运动,连接DE.设点E的运动时间为t(s),△BDE的面积为S(cm2)(这里规定:线段是面积为0的几何图形).
如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,点D为BC的中点,动点E从点A出发,沿着A→B→A的方向以1cm/s的速度运动,当回到点A时停止运动,连接DE.设点E的运动时间为t(s),△BDE的面积为S(cm2)(这里规定:线段是面积为0的几何图形).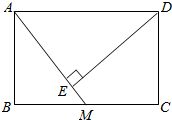 矩形ABCD中,M是BC的中点,DE⊥AM,E是垂足.
矩形ABCD中,M是BC的中点,DE⊥AM,E是垂足.