Question

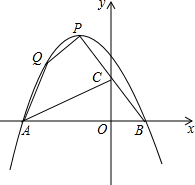如图，已知顶点为P的抛物线y=ax²-x+c经过点Q（-2，

3

2

），其对称轴为直线x=-1，抛物线与x轴相交于A、B两点．
（1）求抛物线的解析式；
（2）求A、B两点的坐标；
（3）设PB与y轴交于C点，求线段AC的长．

Answer 1

考点：二次函数综合题

专题：

分析：（1）由对称轴可求出a的值，再把Q点的坐标代入求出c的值即可求出抛物线的解析式，
（2）令y=0，求出方程x的两个值即可得出点A，B的坐标．
（3）先求出顶点P的坐标，可得出PB所在的直线的解析式，利用y=0，得出点C的坐标，再运用勾股定理求出AC的长．

解答：解：（1）∵y=ax²-x+c，其对称轴为直线x=-1，
∴-

-1

2a

=-1，解得a=-

1

2

，
∴y=-

1

2

x²-x+c，
∵抛物线y=-

1

2

x²-x+c经过点Q（-2，

3

2

），
∴-2+2+c=

3

2

，解得c=

3

2

．
∴抛物线的解析式：y=-

1

2

x²-x+

3

2

，
（2）令y=0，得-

1

2

x²-x+

3

2

=0，解得x₁=1，x₂=-3．
所以点A的坐标为（-3，0），点B的坐标为（1，0），
（3）∵抛物线y=-

1

2

x²-x+

3

2

的顶点为P，
∴点P的坐标为（-1，2）．
∵点B的坐标为（1，0），
设PB所在的直线的解析式为y=kx+b，
∴

2=-k+b 0=k+b

，解得

k=-1 b=1

，
∴PB所在的直线的解析式为y=-x+1，
∵PB与y轴交于C点，
∴点C的坐标为（（0，1），
∵点A的坐标为（-3，0），
∴在RT△AOC中，AC=

AO2+CO2

=

32+12

=

10

．

点评：本题主要考查了二次函数与方程、几何知识的综合应用，解题的关键是求出PB所在的直线的解析式，利用解析式求出点C的坐标．