题目内容
用3根火柴棒搭成1个三角形,接着用火柴棒按如图所示的方式搭成2个三角形,再用火柴棒搭成3个三角形、4个三角形…

(1)填写表:
(2)填空:照这样的规律搭下去,搭n个这样的三角形需要 根火柴棒.
(3)计算:根据(2),搭2013个三角形共需要多少根火柴棒?

(1)填写表:
| 三角形个数 | 5 | 6 | 7 | 8 |
| 火柴棒数 |
(3)计算:根据(2),搭2013个三角形共需要多少根火柴棒?
考点:规律型:图形的变化类
专题:
分析:(1)根据图形找出火柴棒数与三角形个数之间的规律,再根据规律计算即可;
(2)根据(1)的规可直接得出搭n个这样的三角形需要(2n+1)根火柴棒;
(3)根据(2)的公式可将n=2013代入2n+1,求值即可.
(2)根据(1)的规可直接得出搭n个这样的三角形需要(2n+1)根火柴棒;
(3)根据(2)的公式可将n=2013代入2n+1,求值即可.
解答:解:(1)填写下表:
故答案为:11,13,15,17;
(2)照这样的规律搭下去,搭n个这样的三角形需要(2n+1)根火柴棒;
故答案为:(2n+1).
(3)当n=2013时,由2n+1=2×2013+1=4027根,
则搭2013个三角形共需要4027根火柴棒.
| 三角形个数 | 5 | 6 | 7 | 8 |
| 火柴棒数 | 11 | 13 | 15 | 17 |
(2)照这样的规律搭下去,搭n个这样的三角形需要(2n+1)根火柴棒;
故答案为:(2n+1).
(3)当n=2013时,由2n+1=2×2013+1=4027根,
则搭2013个三角形共需要4027根火柴棒.
点评:此题考查了图形的变化类,关键是通过观察图形,得出火柴棒数与三角形个数之间的规律.

练习册系列答案
相关题目
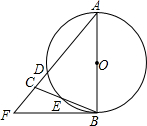 如图,在△ABC中,AB=AC=10,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=
如图,在△ABC中,AB=AC=10,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=| 1 |
| 2 |
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列说法中正确的是( )
| A、两个有理数的差一定小于被减数 |
| B、一对相反数的平方也互为相反数 |
| C、数轴上的点不都表示有理数 |
| D、倒数等于本身的数是+1、-1、0 |
 如图,抛物线y=kx2-2kx-3k交x轴于A、B两点,交y轴于点C,已知OC=OB.
如图,抛物线y=kx2-2kx-3k交x轴于A、B两点,交y轴于点C,已知OC=OB.

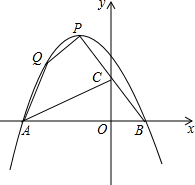 如图,已知顶点为P的抛物线y=ax2-x+c经过点Q(-2,
如图,已知顶点为P的抛物线y=ax2-x+c经过点Q(-2,